Neste post, você aprenderá sobre um dos conceitos mais importantes da estatística frequentista: o valor de p (p-value). Primeiramente, definiremos probabilidade condicional e valor de p. Em seguida, diferenciaremos a hipótese nula da hipótese “zero”. Além disso, exploraremos falácias comuns sobre o valor de p, alternativas a essa métrica e como relatar essa estatística corretamente em sua seção de resultados. Ao longo do texto, apresentaremos exemplos visando esclarecer o uso e a importância do valor de p na pesquisa científica.
O que é uma probabilidade condicional?
A letra p no termo valor de p (p-value) se refere a uma probabilidade condicional. Desse modo, antes de entendermos o valor de p, precisamos compreender o que é uma probabilidade condicional.
Considere dois eventos, A e B. A probabilidade condicional é a probabilidade de um evento ocorrer, dado que outro evento já ocorreu. Denotamos a probabilidade condicional de A, dado que B ocorreu, como p(A | B).
Por exemplo, imagine que a probabilidade de uma pessoa testar positivo para dengue, dado que ela apresenta febre e dores no corpo, seja 0,30. Nesse caso, a probabilidade de testar positivo está condicionada à presença de sintomas. Em outras palavras, é possível que p(“positivo” | sintomas) seja diferente de p(“positivo”).
Para os fins deste post, dois pontos são essenciais. Primeiro, p(“positivo” | sintomas) não nos informa a probabilidade dos sintomas, ou seja, p(sintomas). Quando afirmamos que a probabilidade de testar positivo para dengue, dado que há sintomas, é 0,30, estamos assumindo que os sintomas estão presentes.
Segundo, p(“positivo” | sintomas) não é o mesmo que p(sintomas | “positivo”). Portanto, os valores dessas probabilidades não precisam ser iguais. Veremos outro exemplo adiante que aprofundará essa ideia.

Qual é a definição do valor de p?
Definição do valor de p
O valor de p é a probabilidade de observar uma estatística de interesse igual ou mais extrema que a observada nos dados, assumindo que a hipótese nula é verdadeira. Formalmente, expressamos isso como p(Dados | H0), onde H0 é a hipótese nula.
Essa definição pode parecer complexa à primeira vista. Para facilitar o entendimento, vamos propor um experimento mental.
Proposta de um experimento mental
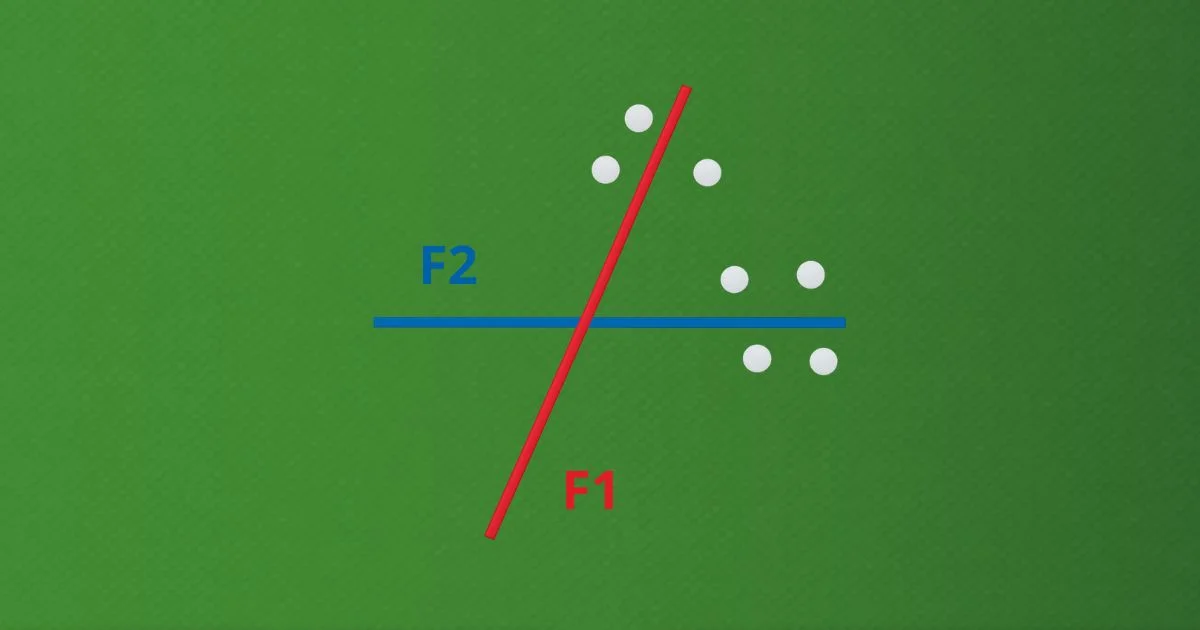
Em nosso experimento mental, vamos assumir algumas premissas. Primeiramente, assumiremos que podemos dividir o estado do mundo em duas categorias, representadas pelas duas colunas da Figura 1.

Na primeira categoria, assumimos que uma variável não tem efeito sobre outra. Ou seja, não há associação, correlação ou mediação entre elas. Isso significa que o valor de uma variável não ajuda a prever o valor da outra. Chamamos essa situação de H0 verdadeira. Na segunda categoria, consideramos o oposto: existe associação, correlação ou mediação, o que define a H0 falsa.
Além disso, outra premissa do experimento mental é de que não sabemos o verdadeiro estado do mundo. Por isso, conduzimos pesquisas; para tomarmos decisões sobre o mundo real minimizando nossas chances de erro. Queremos optar pelas decisões corretas, que estão nas células da diagonal secundária da Figura 1 (rejeição correta e não rejeição correta).
Por fim, a terceira premissa de nosso experimento mental é de que, em nossos estudos, nós inicialmente afirmamos a hipótese nula. Em outras palavras, nós assumimos que ela é verdadeira de antemão. Com base nisso, nós usamos um modelo estatístico que descreve o que poderíamos esperar, em termos de resultados, se a hipótese nula for verdadeira.
Descrição do experimento mental
Vamos tornar isso mais concreto com um exemplo. Suponha que o papagaio Kiwi (Figura 2) foi treinado para dizer apenas duas palavras: “menino” e “menina”. O tutor de Kiwi afirma que seu papagaio consegue prever o sexo biológico de bebês de mulheres grávidas usando essas duas palavras. No experimento, colocamos Kiwi diante da foto de uma mulher grávida e registramos a primeira palavra que Kiwi diz como seu “palpite” do sexo do bebê.

Em nosso experimento mental, temos as seguintes hipóteses:
- Hipótese nula: Kiwi não é capaz de prever o sexo dos bebês. Em outras palavras, o desempenho de Kiwi deve ser o equivalente ao lançamento de uma moeda no cara ou coroa;
- Hipótese alternativa: Kiwi é capaz de prever o sexo dos bebês. Em outras palavras, o desempenho de Kiwi deve ser superior ao lançamento de uma moeda no cara ou coroa.
Essas hipóteses representam os dois possíveis estados do mundo, mas não sabemos qual deles é verdadeiro.
Agora, considere que expomos Kiwi a fotos de 10 mulheres grávidas e registramos os palpites dele. Se Kiwi for incapaz de prever o sexo dos bebês, esperaríamos que ele acertasse a resposta aproximadamente 50% das vezes.
No entanto, em 10 tentativas, Kiwi pode ter sorte e acertar 6 ou 7 respostas, por exemplo. Isso seria suficiente para acreditarmos que ele é capaz de prever o sexo dos bebês? Por outro lado, Kiwi pode ter azar e errar mais do que o esperado, acertando apenas 3 ou 4 respostas. O que precisamos saber é como calcular a probabilidade desses diferentes resultados hipotéticos.
Modelo estatístico sob a hipótese nula
Assumindo que a hipótese nula é verdadeira, podemos usar um modelo estatístico para descrever os possíveis resultados de nosso experimento mental. Em nosso exemplo, esse modelo segue uma distribuição binomial. A Figura 3 mostra as probabilidades de diferentes resultados, caso o papagaio Kiwi não tenha poderes paranormais. Resultados próximos a 50% (5/10 acertos) são mais prováveis, enquanto resultados muito altos (10/10 acertos) ou baixos (0/10 acertos) são improváveis.
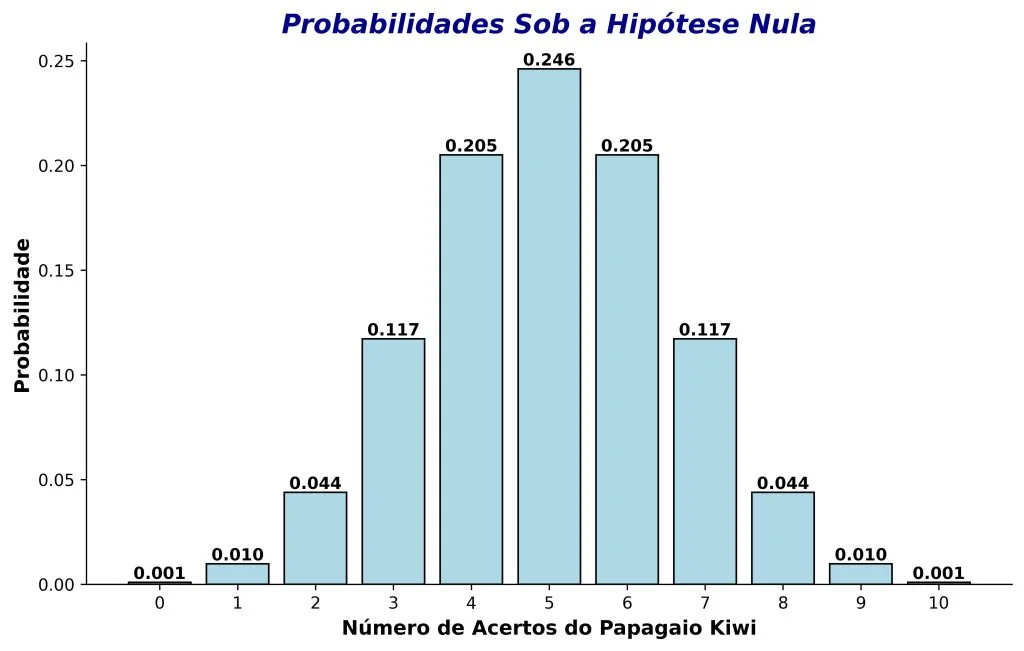
Outra maneira de interpretar a Figura 3 é em termos de quão surpreendentes seriam diferentes resultados sob a hipótese nula. Quanto mais improvável um resultado é de acontecer, mais surpreende ele será, caso de fato ocorra. Na Figura 3, os resultados mais surpreendentes são 0/10 acertos e 10/10 acertos, ambos com uma chance em 1000 cada de acontecer (i.e., 0,001).
Agora, precisamos definir um nível de significância (α, letra grega alfa), que geralmente é de 0,05 em ciências sociais. Esse valor determina o quanto um resultado precisa nos surpreender para rejeitarmos a hipótese nula. O alfa também indica a probabilidade de cometermos um erro Tipo I, ou seja, de rejeitarmos a hipótese nula quando ela é verdadeira. Em outras palavras, um erro Tipo I consistiria em afirmar que o papagaio Kiwi é capaz de prever o sexo dos bebês, quando ele de fato é incapaz de fazê-lo.
Comparação dos dados observados com o esperado sob a hipótese nula
Por fim, vamos calcular o valor de p com base nos dados observados. Suponha que, em nosso experimento, Kiwi acertou 8 de 10 palpites. O valor de p, portanto, será a probabilidade de observar esse resultado, ou resultados mais extremos, dado que a hipótese nula é verdadeira.
A Figura 4 destaca na cor vermelha os resultados iguais ou mais extremos que o observado.
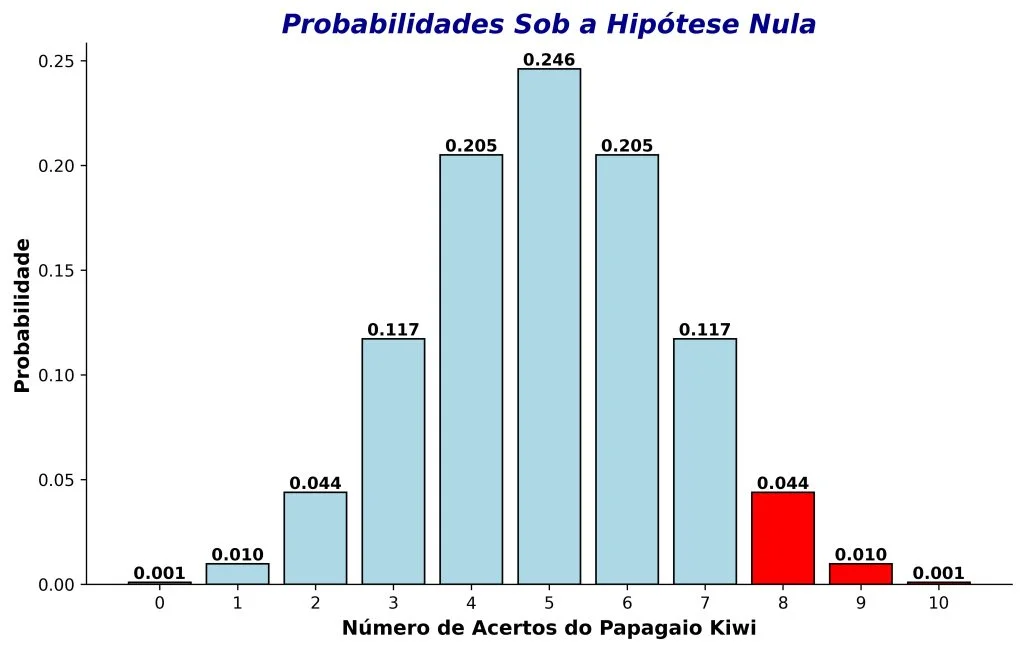
Aqui, o valor de p = 0,044 + 0,01 + 0,001 = 0,055. Como esse valor é maior que nosso alfa de 0,05, não rejeitamos a hipótese nula. Alguns pesquisadores interpretam resultados um pouco acima do alfa como marginalmente significativos, mas evitamos essa interpretação neste post (cf. Kazdin, 2016).
Resumo intermediário
Vamos resumir o que aprendemos até agora sobre o teste de significância da hipótese nula:
- O mundo pode ser dividido em dois estados: hipótese nula verdadeira e hipótese nula falsa;
- Assumimos inicialmente que a hipótese nula é verdadeira;
- Especificamos um modelo estatístico que mostra a probabilidade de diferentes resultados sob a hipótese nula;
- Definimos um nível de significância para determinar quando devemos nos surpreender;
- Coletamos dados e calculamos o valor de p;
- Comparamos o valor de p com o alfa para decidir se rejeitamos ou não a hipótese nula. Se p for menor ou igual ao alfa, rejeitamos a hipótese nula. Se p for maior que alfa, não rejeitamos a hipótese nula.
Qual é a diferença entre hipótese nula e hipótese “zero”?
Considere as seguintes hipóteses: (a) a correlação entre as variáveis A e B é zero; (b) o coeficiente de regressão de X preditivo de Y é paralelo ao eixo x; e (c) as médias de uma variável dependente não diferem entre os Grupos 1 e 2.
Esses são exemplos de hipóteses “zero” (nil hypothesis). Em particular, elas consistem em hipóteses nulas de (a) não correlação, (b) não predição e (c) igualdade de médias. Contudo, é relevante notar que a hipótese nula não precisa ser uma hipótese “zero”.
De fato, o termo nula se refere à hipótese que o pesquisador deseja nulificar ou falsear. No exemplo do papagaio Kiwi, outro pesquisador, o Dr. Cético, poderia defender que mesmo 70% de acertos não seria evidência convincente o suficiente para aceitarmos que o papagaio Kiwi é capaz de prever o sexo de bebês.
Nesse caso, o Dr. Cético poderia estabelecer que a hipótese a ser nulificada seria mais bem representada pela distribuição de probabilidades da Figura 5.
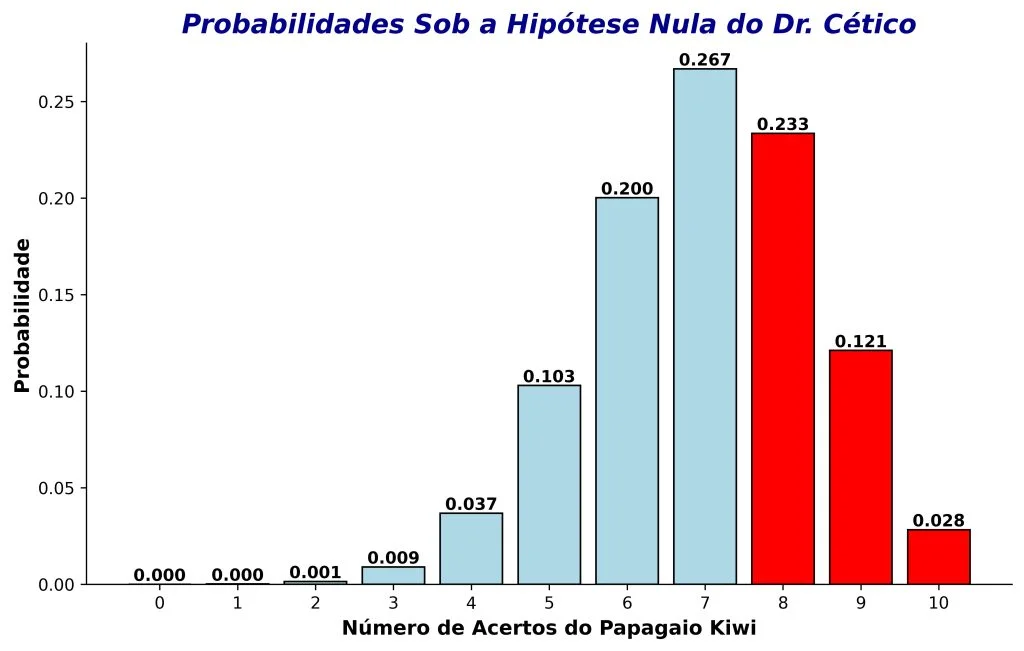
A Figura 5 também foi modelada por meio de uma distribuição binomial. No entanto, essa distribuição está centralizada no valor 7, com assimetria negativa (ou seja, cauda longa à esquerda da distribuição). Além disso, os valores de probabilidade associados a cada possível resultado também mudaram. Sob a hipótese nula do Dr. Cético, o valor de p de nosso experimento seria dado por 0,233 + 0,121 + 0,028 = 0,382.
Em outras palavras, os 8 acertos de Kiwi são pouco surpreendentes se assumirmos que a hipótese nula equivale a acertar 70% das tentativas. Aqui, não rejeitamos a hipótese nula e, além disso, sequer cogitamos afirmações sobre “significância marginal”.
Em síntese, nem toda hipótese nula precisa ser uma hipótese “zero”, conforme mostramos no exemplo do Dr. Cético.
O que significa quando o valor de p é menor que alfa?
Um novo cenário para o experimento mental
Em ciências sociais e comportamentais, três critérios de significância principais são mais comumente adotados pela comunidade científica: 1%, 5% e 10%. Nesse contexto, o termo significância estatística é sinônimo de p ≤ α. O valor de 5%, o mais comumente adotado, foi estabelecido de forma arbitrária, refletindo, em certa medida, as preferências de Sir Ronald Fisher, um dos nomes mais importantes da estatística na primeira metade do século XX.
Relembrando: assumimos que a hipótese nula é verdadeira, realizamos um experimento, e o valor de p nos informa o quão surpreendentes são os nossos resultados. Voltemos mais uma vez ao experimento mental do papagaio Kiwi e à hipótese nula original.
No entanto, agora suponha que o papagaio Kiwi acertou o sexo de 9 de 10 bebês (Figura 6). Sob o novo cenário, o valor de p é dado por 0,01 + 0,001 = 0,011, que é menor que nosso alfa de 0,05.
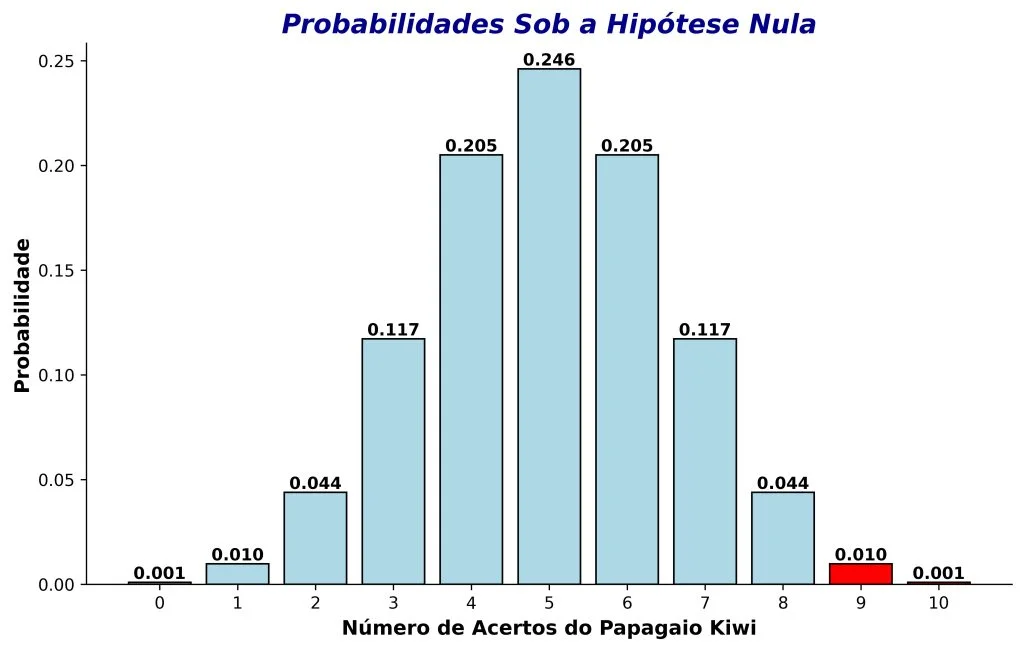
Como interpretamos esse resultado? Em seguida, veremos a resposta.
Como interpretar p menor que alfa?
Existem duas maneiras de conceber o valor de p. Primeiramente, é surpreendente que o papagaio Kiwi tenha acertado 90% das tentativas, pois isso seria esperado em apenas 11 de 1.000 experimentos (p = 0,011). Apesar disso, não deixaremos de acreditar na hipótese nula como uma boa descrição do mundo real.
A segunda é que, se de fato observamos um resultado mais surpreendente do que admitiríamos, isso talvez reflita o fato de que a hipótese nula não é uma boa descrição do mundo real. Nesse caso, rejeitamos a hipótese nula como uma descrição acurada do mundo. Essa segunda alternativa é exatamente a que adotamos quando fazemos testes de hipótese.
Desse modo, se o valor de p for menor ou igual ao nível de significância, rejeitaríamos a hipótese nula e concluiríamos que há evidências suficientes para apoiar a hipótese alternativa de que o papagaio Kiwi é capaz de prever o sexo de bebês. Entretanto, se o valor de p for maior que o alfa adotado, a hipótese nula não seria rejeitada. Isso implica que não há evidências suficientes para rejeitá-la.
Fatores que afetam a escolha do nível de significância
A escolha do nível de significância depende de vários fatores, como:
- A importância da questão de pesquisa;
- As consequências de cometer um erro de falso positivo (erro Tipo I);
- O conhecimento prévio ou expectativas sobre o fenômeno;
- O tamanho da amostra e a variabilidade dos dados.
Em geral, você deve escolher um nível de significância mais baixo (como 0,01 ou 0,001) se você:
- Antever que os resultados da pesquisa têm implicações práticas sérias;
- Desejar minimizar o risco de cometer um erro de falso positivo (erro Tipo I);
- Tiver um tamanho de amostra grande e baixa variabilidade nos seus dados;
- Tiver fortes evidências ou razões para acreditar que a hipótese nula é verdadeira.
Considere o último critério. O seguinte aforismo é atribuído ao astrônomo Carl Sagan: “afirmações extraordinárias requerem evidências extraordinárias”. Por exemplo, no caso de fenômenos paranormais, é razoável exigirmos evidências mais convincentes para rejeitarmos a hipótese nula de que a paranormalidade não explica fenômenos do mundo físico.
O que o valor de p não diz?
Esta seção busca desmistificar algumas falácias sobre o valor de p. Como vimos anteriormente, o valor de p se refere à probabilidade de observamos dados iguais ou mais extremos aos nossos, considerando a hipótese nula verdadeira. A seguir, discorreremos sobre algumas informações que o valor de p não é capaz de nos dar. Para uma lista mais extensa, recomendamos a leitura de Nickerson (2000).
O valor de p não se refere à probabilidade da hipótese nula ser verdadeira
No teste de significância da hipótese nula, não testamos os dados, mas sim a probabilidade dos dados, ou dados mais extremos, considerando a veracidade da hipótese nula.
Pesquisadores diferenciam entre duas probabilidades condicionais, p(Dados | H0) e p(H0 | Dados). Um problema do teste de significância da hipótese nula é muito bem descrito por Cohen (1994, p. 997, livre-tradução):
O que há de errado com o teste de significância da hipótese nula? Bem, entre muitas outras coisas, ele não nos diz o que queremos saber, e nós queremos tanto saber o que queremos saber que, por desespero, acreditamos que sim! O que queremos saber é: “Dados os dados, qual é a probabilidade de que H0 seja verdade?“ Mas como a maioria de nós sabe, o que ele nos diz é: “Dado que H0 é verdadeira, qual é a probabilidade desses dados (ou mais extremos)?“ Essas duas coisas não são as mesmas.
Em outras palavras, o valor de p informa apenas a probabilidade dos dados condicionada à hipótese nula ser verdadeira, mas não o que gostaríamos de saber: a probabilidade da hipótese condicionada à observação dos dados.
Um exemplo didático da distinção entre essas duas probabilidades é fornecido por Espírito Santo e Daniel (2015), mas ligeiramente adaptado a seguir. A probabilidade de alguém ser falante do português, dado que está lendo este post, p(falante do português | lendo o post), deve ser muito próxima a 1, enquanto a probabilidade de alguém estar lendo este post, dado que é falante do português, p(lendo o post | falante do português), deve ser muito próxima a zero, pois apenas alguns dos milhões de falantes do português no mundo estão interessados em aprender sobre o valor de p.
O valor de p não se refere à probabilidade de a hipótese alternativa ser verdadeira
Até o momento, nosso post pode ter transmitido a ideia imprecisa de que existe uma única hipótese alternativa, que consiste no complemento da hipótese nula. Isso não é exatamente verdade.
Por exemplo, a teoria A pode prever uma correlação moderada entre duas variáveis, r = 0,30, enquanto a teoria B prevê que essa mesma correlação será forte, r = 0,60. Se assumirmos que a hipótese nula é a hipótese “zero” de correlação nula, temos aqui duas instâncias distintas de hipóteses alternativas.
Nesse caso, ainda que rejeitemos a hipótese nula, não faz sentido afirmar que o valor de p se refere à probabilidade de a hipótese alternativa ser verdadeira. Qual das duas hipóteses alternativas? O mesmo valor se aplica a ambas as hipóteses? Como deve ter ficado claro, o valor de p nada tem a dizer sobre a hipótese alternativa.
O valor de p não se refere à probabilidade de uma ou outra teoria estar correta
Dando prosseguimento ao exemplo da seção anterior, se os dados indicassem uma correlação negativa (r < 0), teríamos evidência de que os resultados são surpreendentes ou implausíveis sob a hipótese nula. No entanto, eles são ainda mais implausíveis com base no que as teorias A e B previam, isto é, correlações positivas.
Assim como o valor de p nada tem a dizer sobre a hipótese alternativa, ele não pode ser usado diretamente para estimar a probabilidade relativa de duas ou mais teorias competidoras estarem corretas (para esse fim, precisamos do fator de Bayes). Em síntese, lembre-se sempre de que o valor de p refere-se à probabilidade dos dados; ele nada diz sobre a probabilidade de hipóteses, teorias ou modelos.
Quais são as limitações do valor de p?
O valor de p possui limitações importantes que devemos considerar.
O valor de p é influenciado pelo tamanho amostral
Um tamanho amostral elevado pode fazer com que uma pequena diferença ou efeito atinja significância estatística, mesmo que ele não tenha relevância prática.
Por exemplo, o painel esquerdo da Figura 7 mostra que os escores em uma variável dependente qualquer foram significativamente maiores no grupo tratamento (M = 0,01, DP = 1), quando comparado ao grupo controle (M = 0,009, DP = 1), t(199.998) = 2,23, p = 0,03. Vale ressaltar, contudo, que o efeito foi obtido em uma amostra com 100 mil participantes em cada grupo!
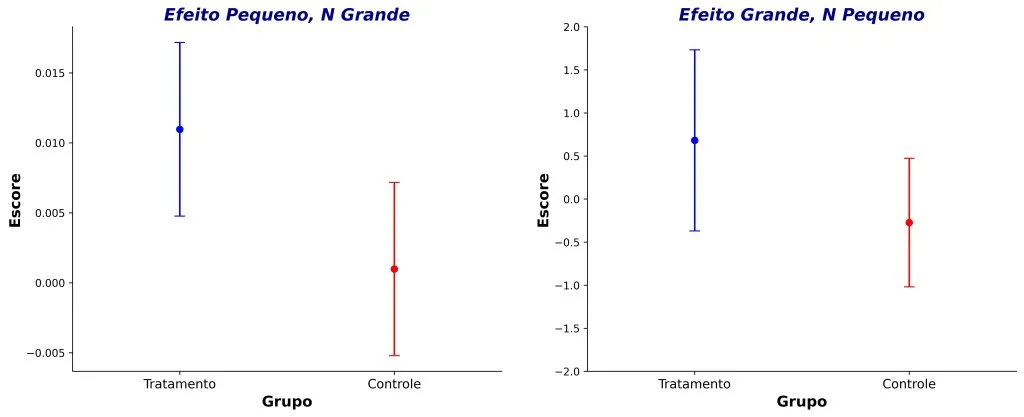
Por outro lado, o painel direito da Figura 7 mostra que os escores em uma variável dependente foi numericamente maior no grupo tratamento (M = 0,68, DP = 1,20), quando comparado ao grupo controle (M = –0,27, DP = 0,85), mas sem atingir significância estatística, t(4) = 1,45, p = 0,18. Isso provavelmente aconteceu porque cada grupo contou com apenas 3 observações.
O valor de p não fornece informações sobre a direção ou magnitude do efeito
O problema dos dados da Figura 7 decorre do fato de que consideramos apenas a decisão dicotômica que o valor de p nos leva a tomar (ou seja, rejeitar ou não rejeitar a hipótese nula). Para compreendermos a importância de um efeito, devemos levar em consideração medidas de tamanho de efeito, como o d de Cohen, o g de Hedges, o Δ (letra grega delta) de Glass, para citar três exemplos.
No painel esquerdo da Figura 7, embora as diferenças entre grupos tenham sido estatisticamente significativas, o tamanho de efeito foi muito baixo (d = 0,01), indicando uma diferença de apenas um centésimo de unidade de desvio-padrão. Por outro lado, as diferenças no painel direito foram de quase uma unidade de desvio-padrão (d = 0,80), embora não tenham atingido significância estatística.
Em estatística, o termo significativo (ou significante) se refere a resultados que geraram um valor de p menor ou igual ao nível alfa. Contudo, um resultado pode ser estatisticamente significativo e não ter importância prática ou teórica, devido à dificuldade de replicação dos achados ou à inviabilidade de traduzir os resultados da pesquisa básica em intervenções que melhorem as vidas das pessoas.
Infelizmente, o uso do termo significativo, em sentido estatístico, se confunde com o uso cotidiano do termo. Por exemplo, na frase “Fulano é uma pessoa significativa em minha vida”, significativo é sinônimo de “importante”. É crucial lembrar que significância estatística não é sinônimo de importância prática. Portanto, recomenda-se cautela na interpretação de resultados com base no valor de p e no uso do termo significativo em relatos científicos.
O valor de p não fornece informações sobre causalidade
O valor de p não nos informa sobre os mecanismos envolvidos na diferença ou efeito que observamos em um estudo. Considerações adicionais – como o delineamento da pesquisa, a existência ou não de variáveis confundidoras e a validade externa dos achados – são necessárias para inferências causais e para explicar como e por que ocorreu a diferença ou efeito.
O valor de p é sensível a múltiplos testes
Realizar muitos testes estatísticos ou explorar muitas variáveis sem hipóteses clara aumentam as chances de encontrarmos resultados estatisticamente significativos por acaso, isto é, de cometermos erros Tipo I. Uma frase recorrente nesse contexto é que “todo dado torturado acaba confessando”. Em outras palavras, se você forçar demais a barra, uma hora os dados acabam “contando” algo, mesmo que isso não faça sentido teórico.
Um relato curioso sobre o problema das comparações múltiplas envolve um estudo em que o sujeito experimental foi colocado em um aparelho de ressonância magnética funcional. Durante o escaneamento do cérebro dele, 15 imagens de humanos em situações sociais foram apresentadas ao sujeito, que foi instruído a tentar determinar a emoção sentida pela pessoa mostrada na foto.
Curiosamente, comparado com uma condição de repouso (sem apresentação de imagens), a apresentação das imagens sociais levou a uma ativação estatisticamente significativa em algumas regiões do cérebro do sujeito (Figura 8). Mais importante: o sujeito experimental era um salmão morto.
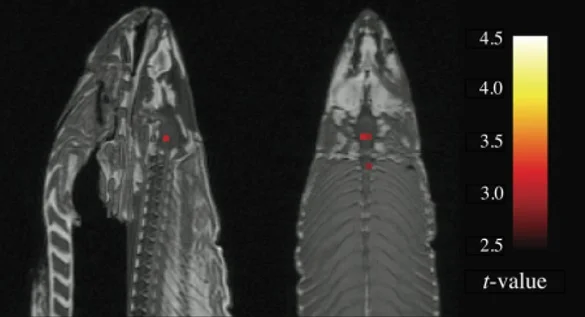
Isso ocorreu porque, em análises de ressonância magnética funcional, as imagens adquiridas são subdivididas em milhares de partes, denominadas voxeis. Ao realizar comparações múltiplas (e.g., milhares de testes t, um em cada voxel), é quase certo que ao menos algumas delas atingirão significância estatística.
A grande mensagem do estudo do salmão, que era exatamente o que os autores pretendiam demonstrar, é que o nível de significância deve ser ajustado para comparações múltiplas (e.g., usando a correção de Bonferroni), de modo que o valor de p seja comparado com um nível de significância ajustado.
Quais são as alternativas ao valor de p?
Existem outras maneiras de testar hipóteses que podem substituir e/ou complementar o valor de p. A seguir, mencionamos três delas.
Estatísticas bayesianas
Essa abordagem utiliza conhecimentos e crenças prévios sobre o fenômeno para atualizar a probabilidade das hipóteses com base nos dados observados.
Em vez do valor de p, análises bayesianas utilizam a distribuição de probabilidade posterior (que reflete a atualização da crença do pesquisador no valor de um dado parâmetro) ou o fator de Bayes (que compara a força relativa da evidência entre hipóteses concorrentes).
Intervalos de confiança
Essa abordagem usa um intervalo de valores que se julga provável conter o verdadeiro valor do parâmetro populacional. Ao invés do valor de p, reporta-se uma estimativa intervalar (e.g., intervalo de confiança de 95% ou 99%) ao redor da estimativa pontual. Essa abordagem é comumente utilizada em revisões metanalíticas.
Tamanhos de efeito
O tamanho de efeito consiste em uma estimativa da magnitude do efeito ou da relação entre variáveis. Em vez de se focar na pergunta dicotômica “existe um efeito?”, como ocorre no teste de significância da hipótese nula, essas estimativas se concentram na pergunta “qual é o tamanho do efeito?”
É recomendável que a apresentação de testes estatísticos sempre inclua medidas de tamanho de efeito, para fornecer mais subsídios à interpretação de resultados de estudos quantitativos.
Como relatar um valor de p?
Ao relatar um valor de p, você deve seguir estas orientações:
- Utilize o sinal de igual (=) se o valor de p for exato, ou use o sinal de menor que (<) se o valor de p for arredondado ou truncado. Tipicamente, um valor de p é apresentado de forma exata até 0,001 (e.g., p = 0,58, p = 0,034, p = 0,02), mas com o “<” quando o valor é inferior a 0,001 (e.g., p < 0,001);
- Use duas ou três casas decimais para o valor de p, a menos que seja muito pequeno ou grande (e.g., p = 0,05 ou p = 0,004, mas não p = 0,0500 ou p = 0,00000004). Use o mesmo número de casas decimais, de forma consistente, ao longo de um texto científico;
- Não use zero como um valor de p, pois é impossível observar um valor de p exatamente zero. É comum, por exemplo, que o SPSS reporte alguns valores de p como “0,000”. Nesses casos, o valor não é exatamente zero. Reporte como p < 0,001;
- Ao interpretar verbalmente o resultado de testes estatísticos, use expressões como “estatisticamente significativo” ou “não estatisticamente significativo”. Quando os resultados não forem estatisticamente significativos, tome cuidado para não afirmar a hipótese nula. Não use expressões como “não existem diferenças entre os Grupos 1 e 2”, pois isso equivale a aceitar a hipótese nula. Falhar em rejeitá-la não é sinônimo de aceitá-la. Seus resultados podem não ter atingido significância por falta de poder estatístico, por exemplo;
- Inclua os graus de liberdade e a estatística do teste (como t, F, χ2) junto com o valor de p e o tamanho de efeito, se aplicável. Por exemplo, t(4) = 1,45, p = 0,18, d = 0,80.
Conclusão
Neste post, fornecemos uma visão abrangente sobre o conceito do valor de p. Ao relatar os resultados de um estudo, é crucial que o pesquisador não se foque apenas no valor de p, mas que também considere medidas de tamanho de efeito, intervalos de confiança e a precisão dos resultados. Entender e interpretar corretamente diferentes estatísticas permite uma avaliação mais precisa e confiável das descobertas de um estudo.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cohen, J. (1994). The Earth is round (p < .05). American Psychologist, 49(12), 997–1003. https://doi.org/10.1037/0003-066X.49.12.997
Espírito Santo, H., & Daniel, F. (2015). Calcular e apresentar tamanhos do efeito em trabalhos científicos (1): As limitações do p < 0,05 na análise de diferenças de médias de dois grupos. Revista Portuguesa de Investigação Comportamental e Social, 1(1), 3–16. https://doi.org/10.7342/ismt.rpics.2015.1.1.14
Figueiredo Filho, D., & Silva, L. (2022). A significância estatística e o uso do p-valor em pesquisas na saúde: Recomendações práticas. Interfaces Científicas – Saúde e Ambiente, 9(1), 230–239. https://doi.org/10.17564/2316-3798.2022v9n1p230-239
Gigerenzer, G. (1993). The superego, the ego, and the id in statistical reasoning. In G. Keren & C. Lewis (Eds.), A handbook for data analysis in the behavioral sciences: Methodological issues (pp. 311–339). Lawrence Erlbaum Associates, Inc.
Kazdin, A. E. (2016). Research design in clinical psychology (5th ed.). Pearson.
Lakens, D. (2022). Improving your statistical inferences. https://doi.org/10.5281/zenodo.6409077
Nickerson, R. S. (2000). Null hypothesis significance testing: A review of an old and continuing controversy. Psychological Methods, 5(2), 241–301. https://doi.org/10.1037//1082-989X.5.2.241
Wasserstein, R. L. & Lazar, N. A. (2016). The ASA statement on p-values: Context, process, and purpose. The American Statistician, 70(2). 129–133. https://doi.org/10.1080/00031305.2016.1154108
Como citar este post
Lima, M. (2024, 15 de janeiro). O que é valor de p? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-valor-de-p/