Neste post, falaremos sobre o teste U de Mann-Whitney. Primeiramente, explicaremos o conceito de postos, que está subjacente ao cálculo da estatística do teste. Nós então apresentaremos um exemplo, que descreve brevemente o objetivo e as hipóteses do teste U de Mann-Whitney. Por fim, nós forneceremos um modelo de como reportar os resultados desse teste estatístico.
O que são postos?
Em síntese, os postos consistem em uma transformação da variável original, onde os escores são ordenados de forma crescente e substituídos por valores que indicam suas posições relativas na sequência.
Por exemplo, suponha que observamos os seguintes escores:
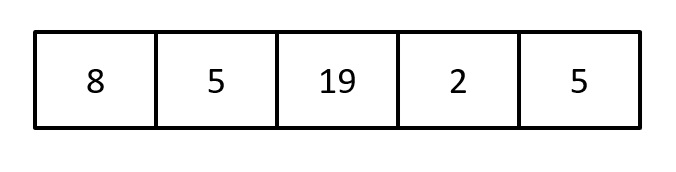
Em seguida, vamos reapresentar esses escores em ordem ascendente:
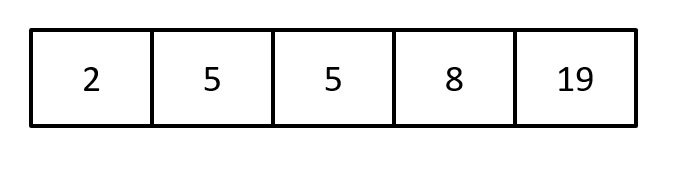
Agora, a transformação dos escores em postos se dará por meio da seguinte regra: ao menor escore, atribuíremos o valor 1; ao segundo menor escore, atribuíremos o valor 2; e assim sucessivamente. Caso existam escores iguais, atribuíremos a cada um deles a média dos postos:

Por exemplo, os postos 2 e 3 estariam associados aos dois escores iguais a 5. Todavia, como não há como determinar a qual escore 5 atribuir o posto 2, e a qual atribuir o posto 3, nós tiramos a média desses postos, (2 + 3) / 2 = 2,5, e atribuímos essa média a todos os postos empatados.
Os postos preservam o ranqueamento relativo dos escores na escala original, mas não as distâncias relativas. Os testes não paramétricos, que se baseiam em postos, podem ser úteis para situações em que a distribuição dos dados é assimétrica (violação do pressuposto de normalidade) ou quando há outliers na amostra.
Além disso, tais testes são úteis quando temos amostras pequenas, inclusive sendo capazes de identificar diferenças que, em certas ocasiões, os correspondentes paramétricos não detectam.

O teste U de Mann-Whitney
O teste U de Mann-Whitney é o equivalente não paramétrico do teste t para amostras independentes. Em outras palavras, ele pode ser usado para comparar diferenças entre duas medidas independentes, usando os postos como desfecho do modelo estatístico.
Antes de prosseguirmos em nossa explicação, é relevante mencionar o teste da soma dos postos de Wilcoxon, criado quase na mesma época que o teste U de Mann-Whitney. Embora usem fórmulas distintas, os dois testes produzem resultados equivalentes. Aqui no blog, preferimos nos referir ao teste U de Mann-Whitney, pois Frank Wilcoxon desenvolveu outro teste, de mesmo nome, aplicável para amostras pareadas.
Qual é a lógica do teste U de Mann-Whitney?
Vamos entender a lógica do teste por meio de um exemplo. Pesquisadores perguntaram a 11 adultos quanto eles gastaram no último presente de Dia das Mães. A Figura 1 apresenta o valor gasto, em reais, por cinco homens (células verdes) e seis mulheres (células vermelhas).

Após ordenarmos de forma ascendente os escores e calcularmos seus postos, temos os dados da Figura 2.
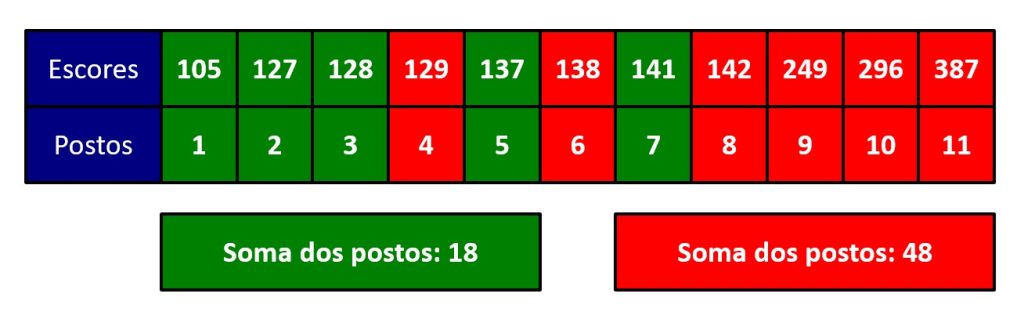
O teste t para amostras independentes é realizado com base nos escores das duas condições, enquanto o teste U de Mann-Whitney é realizado com base nos postos desses escores. Se os grupos não possuem diferenças, esperaríamos os grupos igualmente espalhados ao longo dos postos, isto é, células verdes e vermelhas aproximadamente intercaladas (e soma dos postos aproximadamente iguais).
Em contrapartida, se há diferenças entre os grupos, os valores das somas dos postos deverão diferir. Desse modo, o teste U de Mann-Whitney:
- Calcula os postos dos escores dos dois grupos;
- Soma os postos de cada grupo;
- Calcula dois valores U, um para cada grupo, com base em uma fórmula proposta por Mann e Whitney, e seleciona o menor deles como a estatística do teste.
Não mostraremos a fórmula da estatística U aqui, pois nosso foco é que você compreenda conceitualmente o teste. Mais importante que isso é que você saiba que softwares estatísticos transformam o U em um escore z, que tem um valor de p a ele associado. Esse valor de p indica quão prováveis são os dados, ou dados mais extremos, considerando a hipótese nula verdadeira.
Quais são as hipóteses nula e alternativa do teste U de Mann-Whitney?
Em seguida, chamaremos as duas populações nas quais obtivemos os escores dos grupos de X e Y. Por exemplo, os valores gastos em presentes por homens poderia ser X, e os valores gastos por mulheres poderia ser Y. Com base nessa notação, as hipóteses nula e alternativa do teste U de Mann-Whitney são as seguintes:
- Hipótese nula (H0): para valores aleatoriamente selecionados de X e de Y, a probabilidade de uma observação vinda de X ser maior que uma vinda de Y é igual à probabilidade de uma observação vinda de Y ser maior que uma vinda de X. Em outras palavras, p(Xi) > p(Yi) = p(Yi) > p(Xi);
- Hipótese alternativa (H1): para valores aleatoriamente selecionados de X e de Y, a probabilidade de uma observação vinda de X ser maior que uma vinda de Y é diferente da probabilidade de uma observação vinda de Y ser maior que uma vinda de X. Em outras palavras, p(Xi) > p(Yi) ≠ p(Yi) > p(Xi).
Assim como em outros testes estatísticos, nós definimos um nível de significância (α) e realizamos nossa análise estatística. No caso do teste U de Mann-Whitney, obteremos uma estatística U, um escore z e um valor de p a ele associado. Se p < α, rejeitamos a hipótese nula de que as distribuições das duas populações são idênticas. Em outras palavras, assumimos que há diferenças nos valores gastos no último presente de Dias das Mães entre homens e mulheres.
O teste U de Mann-Whitney compara duas medianas?
Uma concepção amplamente difundida, porém errônea, é que o teste t compara médias (o que está correto), enquanto o teste U de Mann-Whitney compara medianas (essa é a parte da concepção que está incorreta).
Na realidade, o teste U de Mann-Whitney considera tanto a forma quanto o espalhamento dos escores. Note que, em nenhum momento, o cálculo dos postos pressupõe a comparação das medianas dos dois grupos. Em outras palavras, o teste de Mann-Whitney usa mais informações do que simplesmente a mediana.
Como reportar os resultados de um teste U de Mann-Whitney?
A Figura 3 mostra a saída do SPSS de um teste de Mann-Whitney, com base nos dados anteriormente descritos. Se você quer saber como realizar essa análise, então veja nosso post sobre o tema.
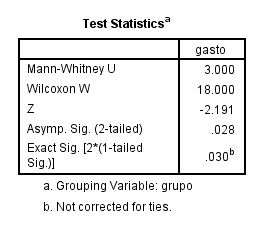
Embora o teste de Mann-Whitney não seja de medianas, podemos reportar medianas e amplitudes (mínimos e máximos) nos resultados, para fins de caracterização descritiva dos grupos, conforme sugerido por Scheff (2016). Além disso, é relevante reportarmos os tamanhos grupais, a estatística U (Mann-Whitney U) e/ou escore z (Z), o valor de p (Exact Sig. [2*(1-tailed Sig.)]). Adicionalmente, Field (2017) recomenda acrescentar uma medida de tamanho de efeito nos resultados.
Em nosso exemplo, a medida de tamanho de efeito será o r, que foi igual a 0,66. Para entender como esse valor foi obtido, veja nosso post sobre o tema.
Desse modo, os resultados descritos a seguir servem como sugestão de redação:
Homens relataram menores gastos com presentes no último Dia das Mães (Mdn = 128 reais, amplitude = 105–141, n = 5) do que mulheres (Mdn = 195,50 reais, amplitude = 129–387, n = 6). O teste de Mann-Whitney identificou diferenças significativas entre os grupos, U = 3, z = 2,19, p = 0,03, r = 0,66, o que indicou um efeito grande, segundo as diretrizes sugeridas por Cohen (1988).
Por fim, é digno notar que um teste t (de Welch) para amostras dependentes, conduzido nesses mesmos dados, indicou que as diferenças entre os grupos não atingiram os níveis convencionais de significância estatística, t(5,21) = –2,21, p = 0,076. Isso corrobora o que foi dito anteriormente, de que, em certas circunstâncias, os testes não paramétricos conseguem detectar diferenças que seus equivalentes paramétricos falham em detectar.
Conclusão
Neste post, você aprendeu mais sobre o teste U de Mann-Whitney o equivalente não paramétrico do teste t para amostras independentes. Gostou desse conteúdo? Então aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Academic press.
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Scheff, S. W. (2016). Nonparametric statistics. In S. W. Scheff (Ed.), Fundamental statistical principles for the neurobiologist : A survival guide (pp. 157–182). Elsevier. https://doi.org/10.1016/B978-0-12-804753-8.00008-7
Como citar este post
Lima, M. (2024, 6 de dezembro). O que é o teste U de Mann-Whitney? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/teste-u-de-mann-whitney/














