Neste post, vamos explorar o que é a comunalidade, como ela se relaciona com a singularidade e por que esses conceitos são fundamentais na análise fatorial exploratória.
Primeiramente, explicaremos a comunalidade, destacando sua definição, interpretação e pontos de corte. Em seguida, abordaremos a singularidade e mostraremos como ela complementa a análise. Por fim, discutiremos como esses dois conceitos ajudam na tomada de decisões ao selecionar ou excluir variáveis em um modelo fatorial.
O que é comunalidade?
Análise fatorial exploratória (AFE) é uma técnica estatística amplamente utilizada na área da psicometria para compreender a estrutura subjacente dos dados observados.
No contexto da AFE, os fatores comuns extraídos no modelo explicam uma proporção da variância de cada variável observada — chamamos essa proporção de comunalidade. Em outras palavras, a comunalidade de um item indica o quanto esse item compartilha sua variância com outros itens do conjunto analisado.
Os valores de comunalidade (h2) variam de 0 a 1. Quanto mais próximo de 1, maior a parte da variância da variável explicada pelos fatores. Sendo assim:
- Comunalidade próxima de 0: sinaliza que a variável tem pouca relação com os fatores comuns. Ela pode estar medindo algo único ou não relacionado ao construto em análise.
- Comunalidade próxima de 1: indica que os fatores comuns representam bem a variável observada. Ou seja, a variável observada compartilha ampla variância com outras variáveis observadas.
Exemplo: suponha que realizamos uma AFE com itens cujos conteúdos abordam autoestima, confiança e motivação. Se esses itens forem explicados por um fator comum, como autoconfiança, então as comunalidades refletirão quanto da variância de cada item é explicada por esse fator.
Pontos de corte para interpretar a comunalidade
Embora os pontos de corte variem conforme o contexto, algumas faixas são geralmente aceitas:
- Acima de 0,70: indicam forte relação dos itens com os fatores comuns. Em outras palavras, as variáveis são representativas da estrutura em estudo.
- Entre 0,50 e 0,70: sugerem uma representação moderada, mas geralmente adequada.
- Abaixo de 0,50: revelam baixa representação pelos fatores comuns. Sendo assim, em tal cenário, deve-se avaliar se a variável realmente contribui para a análise.
O que é singularidade?
A singularidade (ou variância única, u2) é tudo aquilo os fatores comuns não capturam. Em outras palavras, é a fração exclusiva da variabilidade da variável.
Exemplo: Se adicionarmos um item que aborda o tema ansiedade ao conjunto anterior de itens e ele não se correlacionar bem com os itens sobre autoestima, confiança e motivação, então a singularidade do item sobre ansiedade será alta. Isso indicará, portanto, que o fator comum autoconfiança não explica a variância desse item.
A singularidade se divide em duas partes:
- Variância específica: relacionada ao conteúdo particular do item que não é compartilhado com os demais itens. Por exemplo, o item “Sinto-me motivado apenas quando recebo elogios” pode ter uma porção de variância específica ligada à motivação extrínseca, que não está diretamente relacionada ao fator mais geral de autoconfiança.
- Variância de erro (ou erro de medida): variações imprevisíveis, causadas por fatores externos, tais como má interpretação da pergunta, cansaço, distrações etc. Por exemplo, um participante marcou respostas inconsistentes porque, durante o teste, ficou nervoso após lembrar de uma crítica recebida no trabalho — algo que afetou momentaneamente sua autopercepção de confiança.
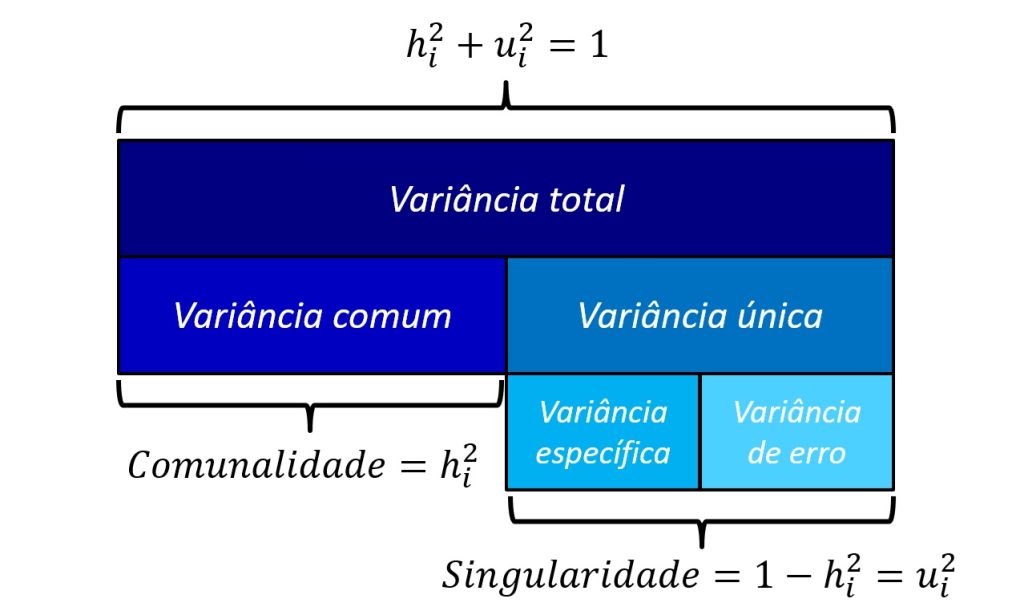
A Figura 1 sumariza a relação entre comunalidade e singularidade. Além disso, ela apresenta outros termos que são tipicamente utilizados quando se aborda o particionamento da variância de itens no modelo do fator comum. Para uma representação alternativa, consulte Damásio (2012), Figura 1.
Pontos de corte para interpretar a singularidade
Assim como ocorre com a comunalidade, a interpretação da singularidade depende do contexto. No entanto, algumas diretrizes são amplamente utilizadas:
- Acima de 0,50: o item apresenta alta singularidade, o que pode indicar que está medindo algo específico, fora da estrutura comum dos demais itens sob análise.
- Entre 0,30 e 0,50: o item tem uma proporção moderada de variância exclusiva.
- Abaixo de 0,30: a maior parte da variância do item é explicada pelos fatores comuns.
Comunalidade e singularidade na prática
A avaliação da comunalidade e da singularidade oferece informações valiosas para interpretar e ajustar modelos fatoriais. Veja como esses indicadores ajudam em diferentes decisões analíticas.
Comunalidade na AFE
A análise da comunalidade permite:
- Identificar variáveis representativas: variáveis com comunalidade elevada são mais alinhadas aos fatores extraídos.
- Selecionar itens relevantes: itens com comunalidades muito baixas podem ser candidatos à exclusão, contribuindo para um modelo mais claro e coeso.
Singularidade na AFE
Já a análise da singularidade ajuda a:
- Detectar variáveis com características únicas: variáveis com alta singularidade podem captar aspectos distintos e complementares ao modelo.
- Tomar decisões fundamentadas sobre inclusão: a exclusão de itens com alta singularidade deve considerar o valor teórico da variável.
Veja também: O que são cargas fatoriais?
Encontrando o equilíbrio entre comunalidade e singularidade
A chave para uma boa AFE está no equilíbrio. Enquanto valores altos de comunalidade favorecem a integração da variável ao modelo, a singularidade também pode ser informativa. Afinal, variáveis com alta singularidade não são necessariamente “ruins” — elas podem captar nuances únicas do construto.
Por exemplo, suponha que, além dos itens sobre autoestima, confiança e motivação, seu instrumento também inclua o item: “Consigo manter a calma mesmo quando recebo críticas”.
Durante a AFE, esse item apresentou alta singularidade (por exemplo, u2 = 0,58), o que indica que apenas 42% da sua variância foi explicada pelos fatores comuns. Em termos estatísticos, isso pode parecer um motivo para excluí-lo. No entanto, teoricamente, esse item pode captar um aspecto específico e valioso do fator autoconfiança: a resiliência emocional diante de críticas — algo que não está fortemente refletido nos demais itens do conjunto.
Por isso, a decisão de manter ou excluir uma variável deve se basear tanto em critérios estatísticos quanto na teoria e nos objetivos de sua pesquisa.
Como citar este post
França, A. (2025, 29 de maio). Comunalidade vs. singularidade: Entendendo as diferenças. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/comunalidade-vs-singularidade-entendendo-as-diferencas/
Nos resultados dos aplicativos de AF, onde surge esse índice? No caso do Jamovi, é representado na coluna de “Uniqueness”? Essa é uma informação que pode parecer óbvia, mas, para efeito de relatos, acho positivo constar no post.
Olá, George! Muito obrigado por sempre trazer comentários relevantes nos posts. Estamos atualizando os conteúdos dos posts, e suas contribuições certamente serão consideradas durante essas atualizações. No caso da singularidade, ela costuma ser apresentada na tabela contendo as Cargas Fatoriais (Cross Loadings). No JASP e no jamovi, essa informação aparece em uma coluna cujo nome é Uniqueness ou Singularidade, a depender do idioma de configuração da instalação. Vale notar que, para cada item, a somas dos quadrados das cargas fatoriais + singularidade = 1.
Equipe Psicometria Online.
Salve, Marcos.
Você é da UnB? Acho que você me prestou uma consultoria em uma disciplina no PSTO, confere?
Abraços
Sou eu mesmo, George. Confere! Lembro-me de nossas conversas no LASI. Um abraço!
Equipe Psicometria Online.
Que legal estar colaborando com a Academy, que é uma unanimidade. Abraços.