Quando realizamos uma análise fatorial confirmatória (AFC), um passo essencial é verificar se o modelo proposto representa bem os dados observados. Para isso, utilizamos diversos índices de ajuste. Entre os mais populares estão a SRMR e o RMSEA, que ajudam a avaliar a qualidade do modelo de forma prática e acessível.
Neste post, vamos explorar o que são a SRMR e o RMSEA, para que servem e como interpretá-los corretamente. Primeiramente, explicaremos a SRMR e suas limitações. Em seguida, abordaremos o RMSEA, destacando seus pontos fortes e situações em que pode falhar. Por fim, recomendaremos nosso post sobre índices de ajuste comparativos.
O que é a SRMR?
Primeiramente, é relevante pensarmos em duas matrizes de correlações (ou de variância–covariância, suas versões não padronizadas). A primeira delas é a matriz empírica, isto é, a matriz de correlações entre as variáveis observadas em nosso banco de dados.
Além disso, temos a matriz implicada pelo modelo, ou seja, a matriz de correlações prevista por nosso modelo de AFC. Em síntese, um de nossos objetivos com índices de ajuste é avaliar em que medida as duas matrizes diferem entre si. Quanto menor a discrepância entre as duas matrizes, mais o nosso modelo de AFC captura a estrutura presente nos dados.
Nesse contexto, a raiz quadrada média dos resíduos padronizados (SRMR, standardized root mean square residual) é um índice de “desajuste” absoluto usado na AFC. Seu principal objetivo é verificar o quanto o nosso modelo de AFC falha em reproduzir as correlações observadas na amostra.
Em síntese, a SRMR calcula a discrepância entre as correlações previstas pelo modelo e as observadas nos dados. Se denominarmos o resíduo padronizado — isto é, a diferença padronizada entre as variâncias e covariâncias observadas e as variâncias e covariâncias implicadas pelo modelo de AFC — de ϵ-chapéu (ϵ = epsilon), a SRMR será igual a:

onde t = p(p + 1)/2, representando o número de variâncias e covariâncias únicas em uma matriz de correlações com p variáveis observadas. Assim, a fórmula da SRMR reflete sua definição: calcula-se a raiz quadrada da soma dos resíduos padronizados, dividida pelo número de variâncias e covariâncias na matriz.
Os valores da SRMR vão de 0 a 1. Um valor de 0 indica ajuste perfeito, ou seja, a matriz de correlações do modelo reproduz exatamente a empírica. Portanto, quanto menor a SRMR, melhor o ajuste do modelo.

Limitações da SRMR
Apesar de útil, a SRMR apresenta algumas limitações importantes. Primeiramente, ela não é muito confiável quando aplicado a variáveis categóricas — um cenário típico em instrumentos de autorrelato que adotam escalas Likert.
Além disso, a SRMR é um índice absoluto. Isso significa que ela mede diretamente a distância entre a matriz de covariância estimada pelo modelo e a matriz observada. Esse enfoque, porém, ignora a complexidade do modelo, o que pode ser problemático.
Por exemplo, imagine dois modelos de AFC com o mesmo valor de SRMR — digamos, SRMR = 0,04. Um deles é mais simples, com menos parâmetros livres que serão estimados. O outro é mais complexo. No entanto, a SRMR não diferencia entre os dois modelos, o que pode levar à escolha de modelos desnecessariamente complicados. Por isso, é comum usarmos índices que penalizam modelos mais complexos.
O que é e por que usar o RMSEA?
O raiz do erro quadrático médio de aproximação (RMSEA, root mean square error of approximation) surge justamente para resolver essa limitação. Sua fórmula é apresentada a seguir:
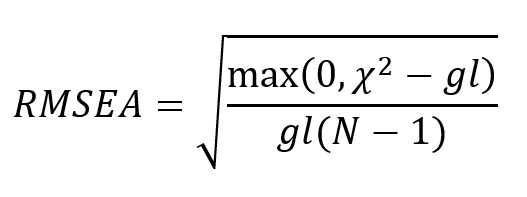
onde χ² é uma medida de ajuste que testa a hipótese nula de igualdade entre as matrizes de variância–covariância observada e implicada pelo modelo; gl representa os graus de liberdade do modelo (ou seja, o número de variâncias e covariâncias observadas menos o número de parâmetros estimados); e N é o tamanho da amostra.
Diferente da SRMR, o RMSEA leva em conta a complexidade do modelo. Em outras palavras, um modelo mais complexo terá mais parâmetros, sendo penalizado na fórmula com um gl menor e, consequentemente, um RMSEA maior.
Além disso, o RMSEA busca estimar o ajuste do modelo à população — e não apenas à amostra.
Entre as vantagens do RMSEA, destacam-se:
- Penaliza modelos mais complexos;
- É menos sensível ao tamanho da amostra, por ser uma estimativa populacional.
Valores do RMSEA também variam entre 0 e 1, sendo que valores menores indicam melhor ajuste. De forma geral, valores abaixo de 0,06 são considerados bons (Brown, 2015), embora exista debate sobre esse ponto de corte.
Por outro lado, o RMSEA pode rejeitar modelos adequados quando o tamanho da amostra é muito pequeno. Nesses casos, convém considerar outros índices de ajuste.
Conclusão
Agora que você entende a SRMR e o RMSEA, é possível usá-los de forma mais estratégica na avaliação de modelos em AFC. Ambos têm seus méritos e limitações. Por isso, é recomendável usá-los em conjunto com outros índices, como o CFI e o TLI.
Saiba mais: CFI, TLI, NNFI: índices comparativos na análise fatorial confirmatória

Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Brown, T. A. (2015). Confirmatory factor analysis for applied research (2nd ed.). The Guilford Press.
Como citar este post
Damásio, B. (2025, 29 de maio). Como interpretar a SRMR e o RMSEA em uma análise fatorial confirmatória? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-interpretar-o-srmr-e-o-rmsea-em-uma-analise-fatorial-confirmatoria/














