As análises estatísticas frequentemente requerem uma profunda compreensão da distribuição de dados. Nesse contexto, dois conceitos fundamentais que você deve compreender são assimetria e curtose.
Essas medidas nos ajudam a descrever a forma de uma distribuição de dados, fornecendo insights valiosos sobre a sua natureza. Neste post, explicaremos ambos os conceitos, oferecendo definições e exemplos para garantir uma compreensão completa sobre o tema.
O que é assimetria?
Definição de assimetria
A assimetria é uma medida de falta de “equilíbrio” de uma distribuição em relação à sua média. Embora pareça tautológico dizer que “assimetria é uma medida de assimetria”, isso acontece porque usamos a mesma palavra para nos referirmos a dois termos distintos do inglês. O conceito asymmetry se refere ao espalhamento dos dados, se homogêneo ou não, ao redor da média; por outro lado, a medida skewness se refere à quantificação do grau de assimetria nos dados. Neste post, o termo assimetria será usado para se referir tanto ao conceito quanto à medida.
Por exemplo, considere o caso da conhecida distribuição normal. Ela consiste em uma distribuição contínua e simétrica, isto é, cujos escores se distribuem de maneira igual ao redor da média. Isso significa que o lado direito da distribuição é uma imagem espelhada do lado esquerdo, conforme ilustra a distribuição normal teórica da Figura 1.
Embora tenhamos exemplificado uma distribuição simétrica utilizando a distribuição normal, é importante notar que existem diversas distribuições de probabilidade que são simétricas, como a distribuição t de Student, a distribuição uniforme e a distribuição de Cauchy, para citar três exemplos.
Classificação quanto à assimetria
Quanto à assimetria, conjuntos de dados podem receber uma de três classificações, a saber, assimetria negativa, simetria e assimetria positiva (Figura 2).
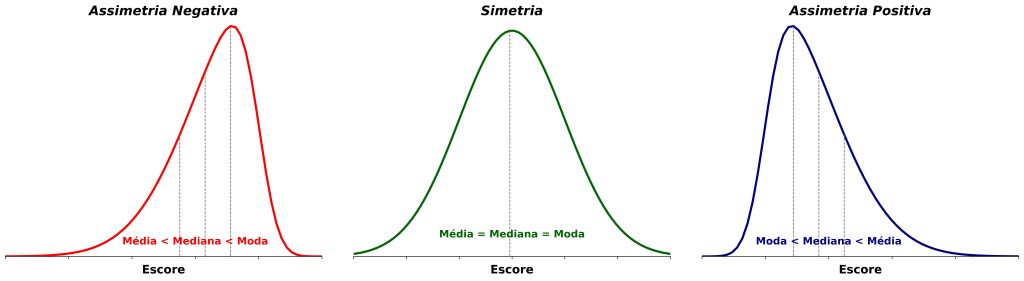
Primeiramente, na assimetria negativa, a cauda esquerda da distribuição é mais longa que a direita (Figura 2, painel esquerdo). Na assimetria negativa, a cauda mais longa aponta na direção dos números negativos da reta real.
Por exemplo, suponha que administramos uma tarefa fácil em uma pesquisa. Desse modo, a maioria dos participantes teve desempenho elevado, enquanto uma minoria obteve escores relativamente baixos.
Em segundo lugar, temos a classificação de simetria, que, como vimos anteriormente, consiste em dados que se distribuem igualmente acima e abaixo da média (Figura 2, painel central).
Muitos fenômenos naturais tendem a se distribuir de maneira simétrica (mais especificamente, seguindo a distribuição normal). Por exemplo, a altura de uma população é bem descrita por uma distribuição normal, onde as frequências de alturas diminuem gradativamente conforme os valores se afastam (para mais ou para menos) da média.
Por fim, na assimetria positiva, a cauda direita da distribuição é mais longa que a esquerda (Figura 2, painel direito). Na assimetria positiva, a cauda mais longa aponta na direção dos números positivos da reta real.
Por exemplo, a renda populacional tem assimetria positiva, pois a maioria da população recebe salários menores, enquanto uma parcela minoritária tem rendas extremamente elevadas.
O que é curtose?
Definição de curtose
A curtose avalia a “caudalidade” do conjunto de dados, ou seja, o quanto há dados concentrados mais nas extremidades da distribuição.
Desse modo, a curtose avalia como os dados se dispersam entre o centro e as caudas de uma distribuição, com valores maiores indicando que uma distribuição de dados pode ter caudas “pesadas”, isto é, que possuem muitas observações.
Por exemplo, podemos ter conjuntos de dados que são simétricos, mas que possuem diferentes graus de espalhamento. Mantidas as médias constantes, o conjunto de dados com com maior variância (ou desvio-padrão) tende a se afastar mais da média, em média.
No entanto, essas medidas de variabilidade não visam quantificar especificamente a quantidade de escores nas caudas, mas sim ao longo de toda a distribuição. Para avaliarmos a caudalidade, usaremos o coeficiente de curtose.
Classificação quanto à curtose
Quanto à curtose, conjuntos de dados podem receber uma de três classificações, a saber, leptocúrtica, mesocúrtica e platicúrtica (Figura 3).
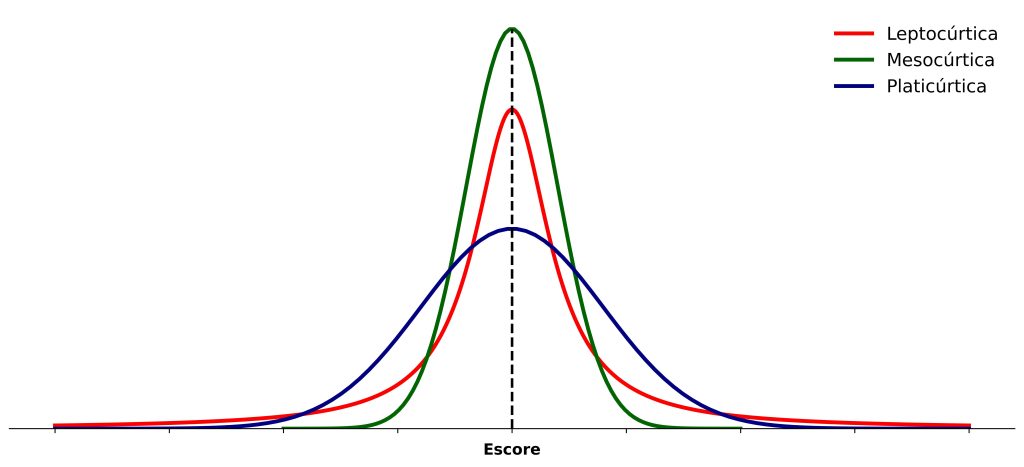
Primeiramente, em uma distribuição mesocúrtica, dizemos que não há excesso de curtose (Figura 3, linha verde). Esse é o caso da já discutida distribuição normal.
Já em uma distribuição leptocúrtica, a distribuição tem excesso positivo de curtose, com caudas mais pesadas (Figura 3, linha vermelha). Em outras palavras, há mais outliers em uma distribuição leptocúrtica do que esperaríamos em uma distribuição normal. Por exemplo, a distribuição t com poucos graus de liberdade é leptocúrtica, pois ela tem caudas mais pesadas que uma distribuição normal.
Por fim, em uma distribuição platicúrtica, a distribuição tem excesso negativo de curtose, em comparação com a distribuição normal. Um exemplo é a distribuição uniforme, onde os diferentes valores são equiprováveis.
Testando a normalidade, incluindo assimetria e curtose
No caso da assimetria, coeficientes negativos indicam assimetria negativa, enquanto coeficientes positivos indicam assimetria positiva. Valores iguais a 0 indicam simetria similar à distribuição normal.
Por outro lado, em relação à curtose, distribuições mesocúrticas têm curtose igual a 0, enquanto distribuições leptocúrticas e platicúrticas têm coeficientes positivos e negativos, respectivamente.
Mas quais valores indicam excesso de assimetria e de curtose? Tabachnick e Fidell (2014) apresentam testes de hipóteses para avaliar assimetria e normalidade. Field (2017) também ensina esses testes que, basicamente, envolvem dividir os coeficientes (de assimetria ou de curtose) por seus respectivos erros-padrões.
De todo modo, Tabachnick e Fidell (2014) recomendam níveis de significância mais conservadores em tais testes (alfa de 0,01 ou de 0,001), mas apenas quando as amostras são pequenas ou moderadas.
No entanto, quando os tamanhos amostrais aumentam substancialmente, testes de hipótese tendem a rejeitar a hipótese nula (de ausências de assimetria e de excesso de curtose) mesmo com desvios pouco importantes. Por esse motivo, Tabachnick e Fidell (2014) recomendam análises gráficas com amostras maiores (e.g., P-P plot, Q-Q plot).
Conclusão
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Tabachnick, B. G., & Fidell, L. S. (2014). Using multivariate statistics (6th ed.). Pearson Education Limited.
Como citar este post
Lima, M. (2024, 12 de dezembro). Assimetria e curtose: Um guia completo. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/assimetria-e-curtose-um-guia-completo/
Prezado Bruno.
Obrigado pelo seu post informativo sobre a curtose. Gostaria apenas de apontar que a figura que você colocou para diferenciar as distribuições mesocúrticas, leptocúrticas e platicúrticas está com as setas invertidas. Segundo sua definição no texto, a curva que deveria ter a seta de platicúrtica é a mais alongada em torno do valor central, ou seja, com poucas caudas. Em todo caso, obrigado pelo seu trabalho… bem didático e esclarecedor.
Olá, Filipe. Agradecemos o comentário. Estamos atualizando posts antigos, de modo a acrescentar mais exemplos. Nós substituímos a figura que você comentou e trouxemos mais exemplos para tentar esclarecer as diferenças quanto aos desvios de curtose. Por exemplo, comparamos agora a distribuição normal à distribuição t, quando falamos de distribuições leptocúrticas. Mais uma vez, muito obrigado pela contribuição!
Equipe Psicometria Online.