A análise de variância (ANOVA) é uma família de testes estatísticos que compara grupos ou condições em função de uma variável quantitativa. No post de hoje, falaremos sobre alguns testes dessa família, conjuntamente conhecidos pelo rótulo guarda-chuva de ANOVA fatorial.
Em seguida, o post estará estruturado da seguinte maneira. Primeiramente, definiremos o termo fator, considerando o contexto da ANOVA. Depois, apresentaremos uma definição geral e um exemplo de ANOVA fatorial. Posteriormente, ampliaremos essa definição, apresentando os diferentes tipos de ANOVAs fatoriais existentes. Nós então apresentaremos as vantagens das ANOVAs fatoriais frente às suas contrapartes unifatoriais. Por fim, apresentaremos os pressupostos das ANOVAs fatoriais.

O que é um fator no contexto da ANOVA?
Infelizmente, a análise quantitativa de dados está repleta de termos polissêmicos — expressões que possuem mais de um significado, a depender do contexto. Neste post, mencionaremos dois desses termos, com foco em seus sentidos no contexto da ANOVA.
Primeiramente, falaremos sobre o termo fator. Abordaremos o segundo termo mais adiante. No contexto da ANOVA, um fator é sinônimo de variável independente, isto é, a variável explicativa em nosso modelo estatístico.
Em inglês, pesquisadores se referem à versão mais simples da ANOVA pela expressão ANOVA one-way. Já em português, traduzimos o termo de múltiplas formas, tais como ANOVA unifatorial, ANOVA de um fator ou ANOVA de uma via. Em todos os casos, o termo se refere ao fato de que esse modelo de ANOVA possui apenas uma variável independente.
Por exemplo, suponha que queremos investigar o efeito do método de ensino (aprendizagem baseada em problemas, aprendizagem colaborativa, sala de aula invertida) sobre a motivação para aprender por parte de estudantes. Nesse cenário, podemos analisar os dados usando uma ANOVA unifatorial.
Para concluir, não confunda o uso do termo fator no contexto da ANOVA, tal como descrevemos nesta seção, com o uso dessa mesma expressão no contexto da análise fatorial.
Qual é a definição de ANOVA fatorial?
A ANOVA unifatorial examina os efeitos de uma variável independente sobre uma variável dependente. Por outro lado, na ANOVA fatorial, examinamos os efeitos de duas ou mais variáveis independentes sobre uma variável independente.
Por exemplo, podemos querer comparar a qualidade do sono em função dos fatores estado civil do participante (solteiro, casado) e horário da prática de exercício (manhã, tarde, noite). Nesse exemplo, temos dois fatores (ou variáveis independentes): estado civil e horário da prática de exercício.
Outra maneira ainda mais explícita de se referir a esse modelo de ANOVA é dizer que conduziremos uma ANOVA fatorial entressujeitos 2 × 3. Primeiramente, o termo entressujeitos indica que cada participante faz parte de apenas um nível de cada uma das variáveis independentes.
Por exemplo, Ana é casada e pratica exercícios de manhã; já Bia é solteira e se exercita à tarde; Cris, por sua vez, é casada e faz exercícios à noite; e assim por diante. Nenhuma das participantes possui mais de um estado civil, nem se exercita em mais de um período.
Agora, passemos à expressão 2 × 3. O número de termos nessa expressão representa o número de variáveis independentes (i.e., duas), enquanto os valores absolutos dos termos representam o número de níveis em cada uma das variáveis independentes. Por exemplo, o 2 indica que estado civil possui dois níveis (solteiro, casado), enquanto o 3 indica que o horário de prática de exercício possui três níveis (manhã, tarde, noite).
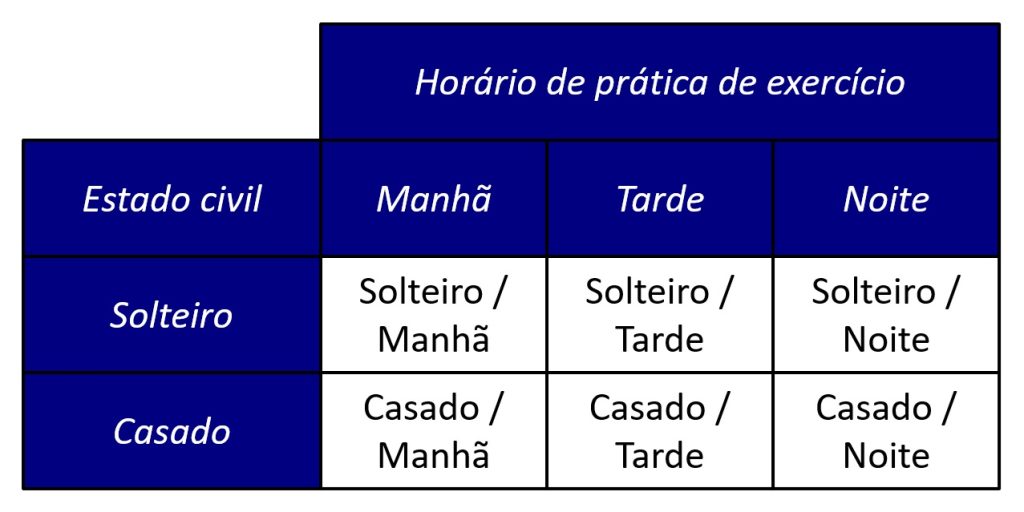
Por fim, o produto resultante dessa multiplicação (2 × 3 = 6) representa o número de grupos ou células em nosso delineamento. O número de células se refere a todos os cruzamentos possíveis de estados civis e de horários de prática de exercício, tal como ilustra a Figura 1.
Quais são os tipos de ANOVA fatorial que existem?
ANOVA fatorial entressujeitos
Na seção anterior, ilustramos o conceito geral de ANOVA fatorial por meio de uma ANOVA fatorial entressujeitos 2 × 3, onde ambos os fatores eram entressujeitos. Em outras palavras, nenhum participante tomava parte em mais de uma condição em cada uma das variáveis independentes.
Vale ressaltar que essa ANOVA também é denominada de ANOVA fatorial de grupos independentes, o que denota o fato de que participantes que estão em determinados grupos não contribuem com escores em outros grupos do delineamento.
ANOVA fatorial intrassujeitos
Existem pelo menos duas possibilidades adicionais de delineamentos. Primeiramente, temos a ANOVA fatorial intrassujeitos, também chamada de ANOVA fatorial de medidas repetidas. O termo intrassujeitos indica que cada participante passa por todos os níveis de uma variável independente.
Por exemplo, suponha que examinemos como o tipo de fundo musical (instrumental, com letra) e a complexidade do texto (simples, complexo) afeta o desempenho em uma tarefa de compreensão de leitura em estudantes universitários.
Considere que cada estudante lerá dois textos simples e dois complexos, sob condições de fundo musical instrumental ou com letra, totalizando quatro medidas de desempenho em tarefa de compreensão de leitura — uma por condição.
Nesse exemplo, podemos analisar nossos dados por meio de uma ANOVA fatorial intrassujeitos 2 × 2. Relembrando, o intrassujeitos se refere ao fato de que todos os estudantes passam por todos os níveis de cada uma das variáveis independentes.
Já o 2 × 2 se refere ao fato de que temos duas variáveis independentes, cada uma delas com dois níveis. O produto resultante dessa multiplicação (2 × 2 = 4) representa o número de condições ou células em nosso delineamento. O número de células se refere a todos os cruzamentos possíveis de tipo de fundo musical e de complexidade do texto, tal como ilustra a Figura 2.

ANOVA fatorial mista
Outro termo polissêmico em análise quantitativa de dados é a palavra mista. Esse termo pode ter diferentes significados, a depender se estamos falando de modelos lineares generalizados, de metanálise ou de ANOVA. Aqui, restringiremo-nos a abordar o sentido do termo no contexto da ANOVA.
O termo misto ocorre quando consideramos variáveis entressujeitos e intrassujeitos em um mesmo modelo analítico. Sendo assim, podemos definir uma ANOVA fatorial mista (às vezes chamada apenas de ANOVA mista ou de split-plot ANOVA) como um modelo estatístico que possui pelo menos uma variável independente entressujeitos e pelo menos uma variável independente intrassujeitos.
Por exemplo, podemos contrastar os efeitos de três psicoterapias (terapia cognitivo-comportamental [TCC], terapia de aceitação e compromisso [ACT], terapia comportamental-dialética [DBT]) sobre os níveis de depressão de pacientes. O tipo de psicoterapia é uma variável independente entressujeitos, pois expomos cada paciente a apenas uma modalidade psicoterápica.
Além disso, mensuraremos os níveis de depressão em três tempos distintos (pré-tratamento, pós-tratamento, follow-up). Sendo assim, entendemos o tempo como uma variável independente intrassujeitos.
Podemos sumarizar esse modelo de ANOVA como uma ANOVA fatorial mista 3 × 3, onde o primeiro 3 representa nossa variável independente entressujeitos, a psicoterapia, com três níveis (TCC, ACT, DBT); e o segundo 3 representa nossa variável independente intrassujeitos, o tempo, também com três níveis (pré-tratamento, pós-tratamento, follow-up).
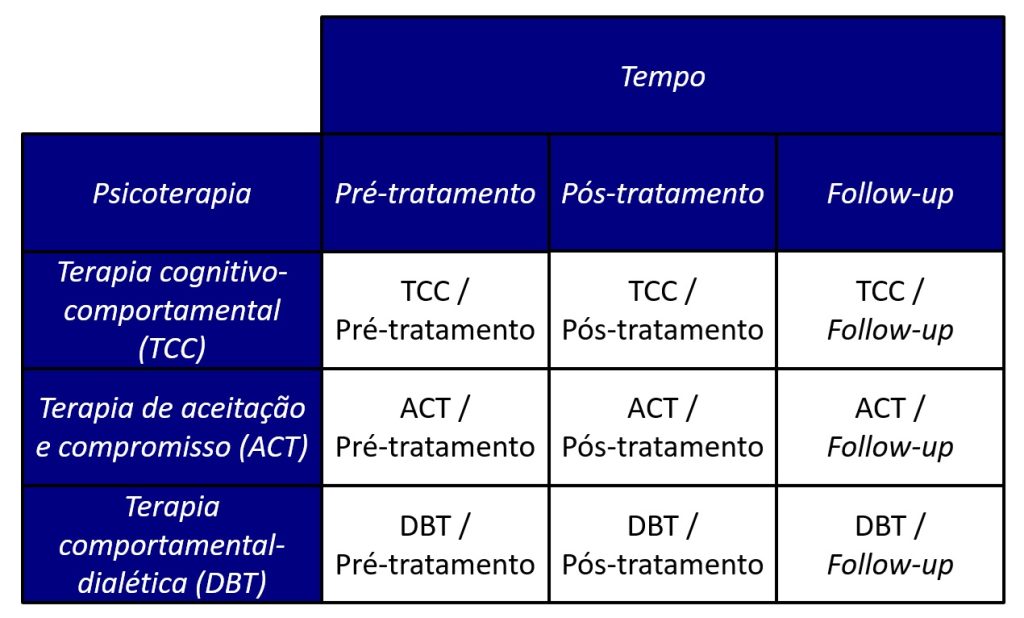
Por fim, o produto resultante dessa multiplicação (3 × 3 = 9) representa o número de condições ou células em nosso delineamento. O número de células se refere a todos os cruzamentos possíveis de tipo de psicoterapia e do tempo, tal como ilustra a Figura 3.
ANOVAs fatoriais com três ou mais variáveis independentes
Todos os exemplos anteriores se focaram em estudos com duas variáveis independentes. No entanto, ANOVAs fatoriais também se aplicam a cenários em que temos três ou mais variáveis independentes.
Por exemplo, podemos examinar os níveis de ansiedade acadêmica de estudantes universitários em dois momentos distintos (início e final do semestre), em função do status ocupacional do estudante (trabalha, não trabalha), do estudante residir ou não com a família (reside, não reside) e da área de seu curso (humanas, exatas, biológicas).
Nesse exemplo, teríamos uma ANOVA fatorial mista 2 × 2 × 2 × 3. Lembre-se que o número de termos desta multiplicação (neste exemplo, 4) indica o número de variáveis independentes, enquanto os valores representam os números de níveis em cada uma das variáveis independentes.
Em nossa ANOVA fatorial mista com quatro fatores, o momento da coleta de dados é um fator intrassujeitos, e os demais fatores (status ocupacional, reside com a família e área do curso) são entressujeitos. Aqui o nosso delineamento teria 24 células, valor calculado pelo produto dos termos da ANOVA fatorial mista.
Qual é a vantagem da ANOVA fatorial sobre ANOVAs de um fator e de medidas repetidas?
Retomemos o exemplo das psicoterapias e níveis de depressão. Teoricamente, poderíamos analisar o efeito das psicoterapias usando uma ANOVA unifatorial. Além disso, poderíamos examinar o efeito do tempo sobre os níveis de depressão usando uma ANOVA de medidas repetidas.
No entanto, as ANOVAs unifatoriais e de medidas repetidas não examinam os efeitos de interação das variáveis independentes.
Já as ANOVAs fatoriais examinam tanto os efeitos principais de cada variável independente (i.e., o efeito de cada variável independente, ignorando as demais variáveis no modelo), como os efeitos de interação — se os efeitos de uma variável independente dependem dos níveis de outra variável independente.
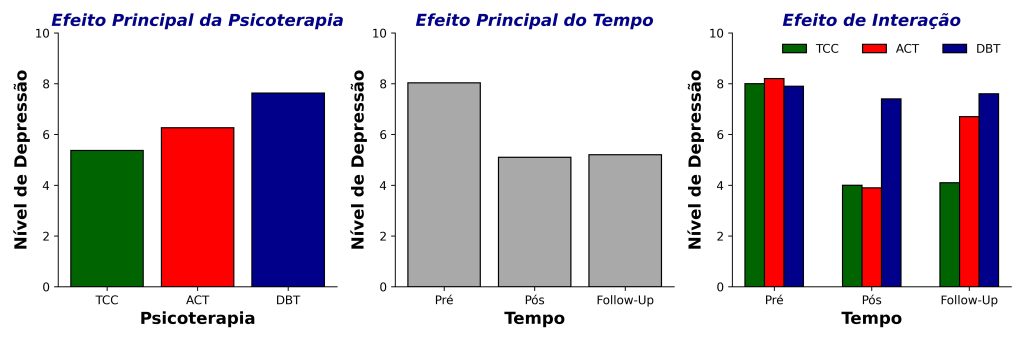
Isso é relevante porque variáveis independentes podem se combinar para produzir seus efeitos sobre uma variável dependente. A Figura 4 ilustra isso. No painel esquerdo, vemos o efeito da psicoterapia, enquanto o painel central ilustra o efeito do tempo. Mais importante, o painel direito indica que o efeito da TCC é mais duradouro que os efeitos da ACT, que declinam no follow-up.
Além disso, as ANOVAs fatoriais contribuem para identificarmos condições limítrofes de um fenômeno. Por exemplo, imagine que um pesquisador demonstre que uma dieta rica em peixe reduz o risco de ataque cardíaco.
No entanto, outra equipe de pesquisa descobre que isso ocorre apenas quando o peixe é grelhado ou assado; se o peixe é frito, o risco aumenta (Belin et al., 2011). Em outras palavras, o modo de preparo é uma variável que define sob quais condições o consumo de peixe protege ou aumenta o risco de ataque cardíaco (Figura 5).

A ANOVA fatorial poderia ajudar a detectar essa condição limítrofe dos efeitos protetivos do consumo de peixe que, em última análise, tem relevância prática.
Quais são os pressupostos das ANOVAs fatoriais?
Para realizar uma ANOVA fatorial, certas pressupostos devem ser satisfeitos. No entanto, tenha em mente que os pressupostos que são relevantes em um caso particular dependem do modelo de ANOVA fatorial que usaremos.
Por exemplo, o pressuposto de esfericidade é relevante apenas quando temos pelo menos um fator intrassujeitos com três ou mais níveis (i.e., ANOVA fatorial intrassujeitos ou ANOVA fatorial mista). O pressuposto de homocedasticidade, por sua vez, aplica-se a fatores entressujeitos (i.e., ANOVA fatorial entressujeitos ou ANOVA fatorial mista).
Os pressupostos estatísticos das ANOVAs fatoriais incluem:
- Normalidade: os resíduos (diferença entre a observação e a previsão do modelo) devem ser aproximadamente normalmente distribuídos.
- Homocedasticidade: a variância dos resíduos deve ser igual em todos os níveis do fator independente.
- Esfericidade: as variâncias das diferenças entre pares de condições de medidas repetidas são aproximadamente iguais. Em outras palavras, a variância da diferenças entre as condições A e B é semelhante à variância das diferenças entre as condições A e C, à variância das diferenças entre as condições B e C, e assim por diante.
- Independência: as observações devem ser independentes umas das outras. Isso geralmente é garantido por um bom desenho experimental.
- Medições em nível intervalar ou de razão: a variável dependente deve ser contínua.
Quando os critérios estabelecidos pelo modelo não são cumpridos, pode-se adotar testes não paramétricos de natureza semelhante. Na linguagem R, os equivalentes não paramétricos das ANOVAs fatoriais são implementados por meio de pacotes como o nparLD e o rankFD.
Conclusão
Neste post, nosso objetivo foi mehorar sua compreensão da família de testes estatísticos conhecida como ANOVA, introduzindo um subconjunto de testes pertencentes a essa família: as ANOVAs fatoriais. Gostou deste conteúdo? Então aproveite e se inscreva em nosso canal no YouTube para ficar por dentro de nossas novidades!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Belin, R. J., Greenland, P., Martin, L., Oberman, A., Tinker, L., Robinson, J., Larson, J., Van Horn, L., & Lloyd-Jones, D. (2011). Fish intake and the risk of incident heart failure: Clinical perspective The Women’s Health Initiative. Circulation: Heart Failure, 4(4), 404–413. https://doi.org/10.1161/CIRCHEARTFAILURE.110.960450
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Como citar este post
Lima, M. (2023, 27 de agosto). O que é ANOVA fatorial? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/anova-fatorial/