O que é análise fatorial confirmatória?

A análise fatorial confirmatória (AFC) é uma técnica estatística essencial para validar a estrutura interna de instrumentos psicométricos. Neste post, vamos explicar o que é AFC, como ela funciona e quais são seus principais elementos.

Primeiramente, revisitaremos o modelo dos fatores comuns. Em seguida, falaremos sobre a especificação do modelo, os métodos de estimação e os índices de ajuste. Por fim, discutiremos como interpretar os resultados da AFC e identificar problemas no modelo.

Entendendo os fatores e o modelo fatorial

Para compreender o que é AFC, é fundamental conhecer o modelo dos fatores comuns. Em síntese, esse modelo parte da ideia de que existe uma ou mais variáveis latentes que influenciam um conjunto de variáveis observáveis. Por exemplo, não podemos medir a depressão diretamente, mas seus efeitos aparecem em sintomas como insônia, fadiga, culpa e alterações no apetite (Figura 1).

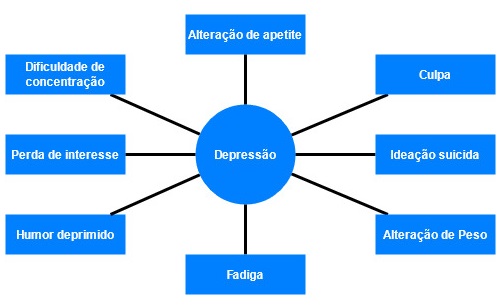
Nesse contexto, a AFC nos permite determinar se o nosso modelo é capaz de explicar as variâncias e as covariâncias entre um conjunto de medidas observáveis. Ou seja, nós entendemos que pessoas com depressão têm aspectos em comum em relação à estes sintomas. Em outras palavras, assumimos que estes sintomas têm uma variação específica e mudam juntos.

Por exemplo, podemos ter um modelo onde acreditamos que uma pessoa com depressão que apresente perda de interesse, fadiga e humor deprimido, também apresentará, em algum grau, dificuldade de concentração, culpa e alteração no apetite.

Como funciona a análise fatorial confirmatória?

Anteriormente, vimos que a AFC é uma técnica que funciona com base em nossas hipóteses. Isto é, quando fazemos uma AFC, iremos determinar todos os aspectos do nosso modelo. Sendo assim, o primeiro passo é justamente identificar e especificar o modelo teórico que queremos testar. Para isso, basta traduzirmos nosso modelo teórico, respeitando algumas limitações.

Na AFC, devemos especificar os fatores, que são as causas teóricas das variáveis observadas. Portanto, não podemos ter fatores sem variáveis associadas, ou fatores com uma só variável observada.

Nós também podemos especificar, em nosso modelo, que os fatores podem se correlacionar. Em contrapartida, se hipotetizarmos que um fator causa o outro (ou seja, que há uma relação direcional dos efeitos de um fator sobre o outro), então estaremos entrando no campo da modelagem por equações estruturais.

Além disso, existem modelos bastante complexos que podem ser estimados por meio da AFC. Neste post, trabalharemos com um exemplo de modelo bem simples, mas é bom ter em mente que existem muitas outras possibilidades de modelagem, tais como:

• AFC com indicadores contínuos e categóricos.
• AFC com múltiplos grupos.
• Fatores de segunda ordem.
• AFC com variáveis mediadoras.
• AFC com variáveis não lineares.

Especificando um modelo de personalidade na análise fatorial confirmatória

Para fins de exemplo, vamos identificar um modelo de personalidade. Selecionaremos cinco itens de neuroticismo e cinco itens de extroversão de um banco de dados.

Em nosso modelo, podemos dizer que existe um fator extroversão, que é a causa de comportamentos como achar fácil falar com outras pessoas; e existe um fator neuroticismo, que é a causa de comportamentos como ficar irritado facilmente. Sendo assim, tal como sugerido por teorias prévias, podemos identificar nosso modelo tal como a representação da Figura 2.

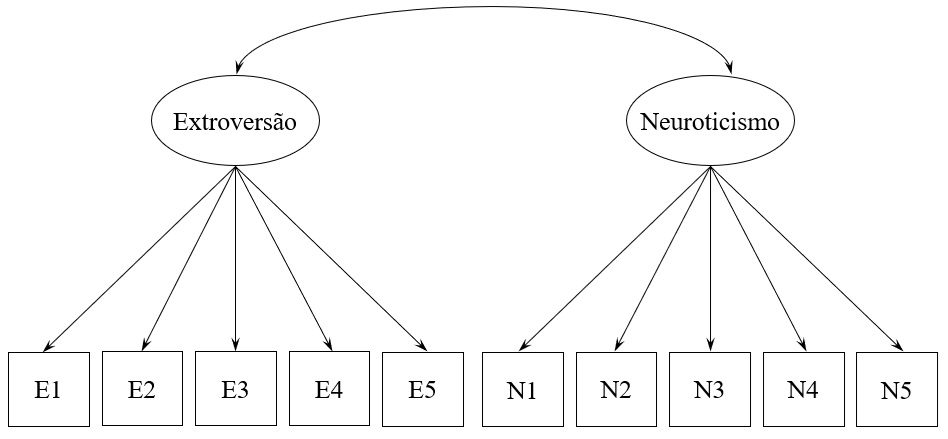
Repare que as setas indicam que os fatores (representados por ovais) são a causa dos comportamentos observados (representados por quadrados). Além disso, há correlação entre os fatores, representada pela seta em ambos os lados.

Existem diversos softwares e pacotes estatísticos que podemos usar para a modelagem de AFC, como o MPlus e o pacote lavaan, do R (que também é utilizado no JASP). Cada um deles tem uma maneira de “traduzir” este modelo de forma que o computador possa entender. Para fins de exemplo, no lavaan ficaria assim:

Extroversao =~ E1 + E2 + E3 + E4 + E5
Neuroticismo =~ N1 + N2 + N3 + N4 + N5

Neste código, estamos dizendo que o fator Extroversao é a causa dos itens E1, E2, E3, E4 e E5. Já o fator Neuroticismo é a causa dos itens N1, N2, N3, N4 e N5. Os nomes dos fatores (Extroversao e Neuroticismo) são arbitrários. Sendo assim, podemos colocar os nomes que quisermos. Já o nome dos itens corresponde aos itens no cabeçalho de nosso banco de dados. O próximo passo será determinar o estimador da AFC.

Estimação dos parâmetros

O objetivo da AFC é estimar parâmetros que indiquem se a estrutura fatorial testada consegue reproduzir, de forma adequada, a matriz de covariância observada nos dados. Em termos mais simples, queremos que o modelo estatístico seja capaz de refletir a estrutura de correlações presente nos dados originais.

Existem diversos métodos possíveis para realizar essa estimação. O mais comum é o método de máxima verossimilhança (maximum likelihood, ou ML), em parte porque ele fornece uma série de estatísticas úteis para a interpretação do modelo. Por exemplo, o ML estima os erros-padrão dos parâmetros, permitindo o cálculo de intervalos de confiança. No entanto, esse método exige que os dados atendam a alguns pressupostos importantes:

• O tamanho da amostra deve ser muito grande.
• Os indicadores (itens) devem ser contínuos.
• A distribuição dos indicadores deve ser normal.

Se não observarmos estes pressupostos, nossos erros-padrão podem aumentar, o que pode nos levar a não rejeitar a hipótese nula, quando ela for falsa. Então, se temos indicadores categóricos ou poucos dados, devemos usar outros estimadores. O ML com estimadores robustos, também chamado de MLM, tem correções para amostras não normais, mas que ainda deve ser grande.

Para variáveis categóricas, existe o weighted least squares e sua versão robusta, o WLSMV (robust DWLS, no lavaan). Também podemos usar esses métodos quando temos indicadores contínuos e amostras pequenas. No entanto, para amostras grandes e indicadores contínuos, o ML e MLM ainda são mais recomendados.

No nosso exemplo, vamos usar o WLSMV, já que os itens da escala são categóricos. Estas recomendações vêm do livro de Brown (2015).

Com o estimador selecionado, podemos fazer os cálculos da AFC. O próximo passo é verificar o quão bem o modelo que escolhemos explica nossos dados. Para fazer isto, vamos olhar os índices de ajuste.

Veja também: Dicas de livros sobre psicometria

Índices de ajuste na análise fatorial confirmatória

Os índices de ajuste são estatísticas que avaliam o quão bem o modelo testado representa os dados observados. Cada índice possui características próprias, com vantagens e limitações. Em seguida, apresentamos os principais índices para uma análise inicial de modelos próprios ou de estudos publicados.

O índice mais tradicional é o qui-quadrado (χ²), que testa a hipótese nula de que a matriz de covariâncias estimada pelo modelo é igual à matriz observada. Um valor de χ² significativo indica má adequação do modelo aos dados. Contudo, esse índice é sensível ao tamanho da amostra — em amostras grandes, tende a ser significativo mesmo com desvios pequenos. Por isso, raramente é interpretado isoladamente.

Dois índices amplamente utilizados são o CFI (comparative fit index) e o TLI (Tucker–Lewis index), que comparam o modelo testado a um modelo nulo. Seus valores variam entre 0 e 1, e interpreta-se que valores acima de 0,95 indicam bom ajuste.

Outro índice importante é o SRMR (standardized root mean square residual), que mede a diferença entre as correlações observadas e as preditas pelo modelo. Quanto menor essa discrepância, melhor o ajuste — idealmente, abaixo de 0,05.

Por fim, o RMSEA (root mean square error of approximation) estima o erro médio de aproximação entre o modelo e a população. Valores inferiores a 0,06 sugerem ajuste adequado.

Esses critérios são amplamente recomendados por autores como Brown (2015) e são um ponto de partida útil para avaliar a qualidade de um modelo.

Quão bom é nosso modelo de análise fatorial confirmatória?

Em nosso modelo, os índices de ajuste estão próximos dos valores considerados como bons, mas ainda não chegamos lá. Nosso χ² foi significativo, χ²(34) = 652,082, p < 0,001, CLI = 0,942, TLI = 0,923, SRMR = 0,071, RMSEA = 0,083, IC 90% [0,078, 0,089]. Portanto, a AFC não corrobora nosso modelo onde extroversão e neuroticismo são as causas latentes dos indicadores que observamos.

A partir disso, podemos investigar o porquê nosso modelo não foi adequado. Pode ser que nossa teoria de personalidade precise de modificações. Por outro lado, é possível que um ou mais itens não sejam bons indicadores dos construtos, segundo a nossa teoria. Uma terceira possibilidade ainda é de que a estrutura que utilizamos, com dois fatores, não seja adequada.

Um próximo passo para termos um modelo melhor é olhar os índices de ajuste. Mas este assunto mais avançado será objeto de um post futuro.

Conclusão

Com este artigo, esperamos que agora você tenha um entendimento geral das primeiras coisas que avaliamos em uma AFC. Principalmente, esperamos que quando você ler um artigo contendo uma AFC, você possa fazer uma análise inicial da qualidade do modelo abordado.

Como este é um assunto bem complexo, cada índice e aspecto citado aqui merece um artigo só para ele, para que possamos aprofundar o assunto. Desta forma, teremos mais domínio sobre as decisões que podemos tomar quando conduzirmos uma AFC. Recomendamos que o próximo passo desta trajetória seja o nosso artigo sobre o SRMR e RMSEA na AFC!

Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).

Referência

Brown, T. A. (2015). Confirmatory factor analysis for applied research (2^nd ed.). The Guilford Press.

Como citar este post

Damásio, B. (2025, 14 de maio). O que é análise fatorial confirmatória? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/analise-fatorial-confirmatoria/