Neste post, falaremos sobre o teste de Kruskal-Wallis. Primeiramente, explicaremos o conceito de postos, que está subjacente ao cálculo da estatística do teste. Nós então apresentaremos um exemplo, que descreve brevemente o objetivo e as hipóteses do teste de Kruskal-Walis. Por fim, nós forneceremos um modelo de como reportar os resultados desse teste estatístico.
O que são postos?
O teste de Kruskal-Wallis é baseado na transformação da variável original em postos. Em síntese, os postos consistem em uma transformação da variável original, onde ordenamos os escores de forma crescente e substituídos por valores que indicam suas posições relativas na sequência.
Por exemplo, suponha que observamos os seguintes escores:
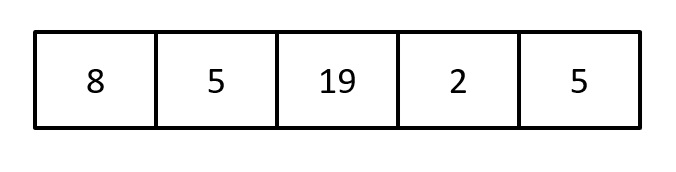
Primeiramente, reorganizaremos esses escores em ordem ascendente:
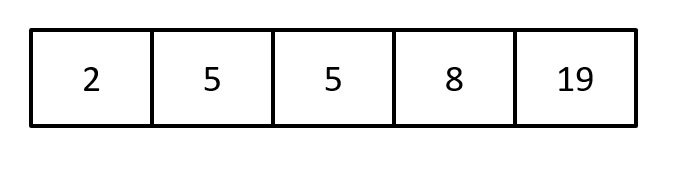
Em seguida, a transformação dos escores em postos se dará por meio da seguinte regra: ao menor escore, atribuíremos o valor 1; ao segundo menor escore, atribuíremos o valor 2; e assim sucessivamente. Caso existam escores iguais, atribuíremos a cada um deles a média dos postos:

Por exemplo, os postos 2 e 3 estariam associados aos dois escores iguais a 5. Todavia, como não há como determinar a qual escore 5 atribuir o posto 2, e a qual atribuir o posto 3, nós tiramos a média desses postos, (2 + 3) / 2 = 2,5, e atribuímos essa média a todos os postos empatados.
Os postos preservam o ranqueamento relativo dos escores na escala original, mas não as distâncias relativas. Os testes não paramétricos, que se baseiam em postos, podem ser úteis para situações em que a distribuição dos dados é assimétrica (violação do pressuposto de normalidade) ou quando há outliers na amostra.
Além disso, tais testes são úteis quando temos amostras pequenas, inclusive sendo capazes de identificar diferenças que, em certas ocasiões, os correspondentes paramétricos não detectam.

O teste de Kruskal-Wallis
O teste de Kruskal-Wallis é o equivalente não paramétrico da análise de variância (ANOVA) de uma via. Primeiramente, vamos lembrar da ANOVA. Nela, nós examinamos se uma variável dependente contínua difere em função de três ou mais grupos independentes. A Figura 1 ilustra a comparação da ANOVA, que compara se pelo menos duas médias (linhas pontilhadas) diferem estatisticamente entre si.
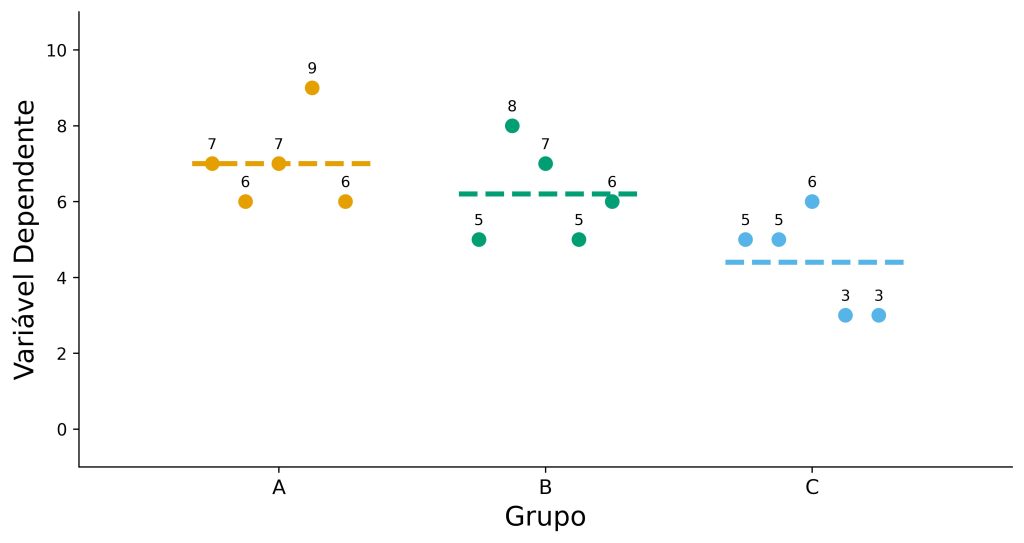
Por outro lado, o teste de Kruskal-Wallis transforma os escores da variável dependente em postos, conforme descrito na seção anterior. Na sequência, compara-se se os postos diferem entre pelo menos dois grupos, conforme ilustramos na Figura 2.
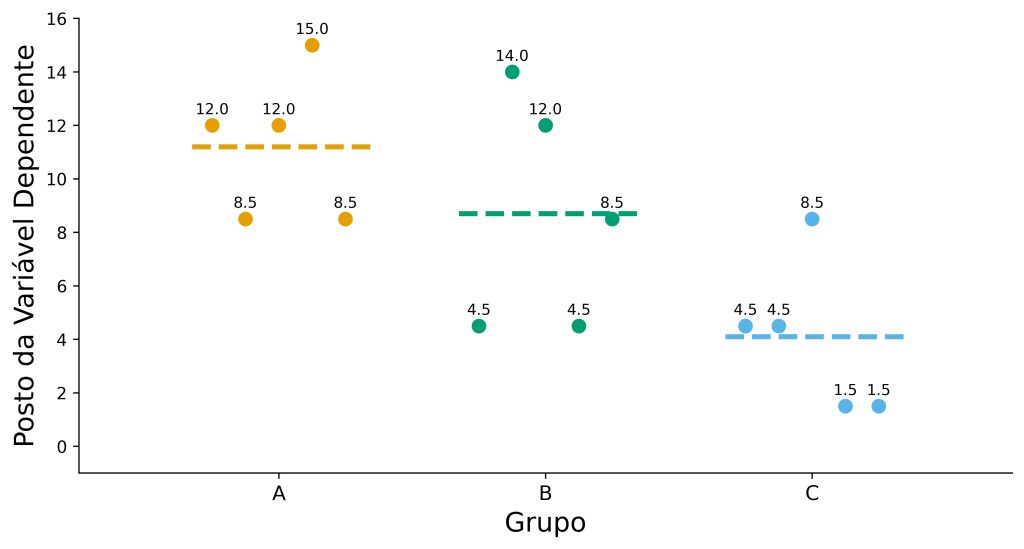
Em outras palavras, podemos usar o teste de Kruskal-Wallis para examinar diferenças entre três ou mais grupos independentes, usando os postos como desfecho do modelo estatístico.
Qual é a lógica do teste de Kruskal-Wallis?
Vamos entender a lógica do teste por meio de um exemplo. Uma psicóloga quer investigar se diferentes intervenções breves de relaxamento têm efeitos distintos na redução do estresse percebido em estudantes universitários.
Ela seleciona 30 participantes, aleatoriamente divididos em três grupos com 10 participantes cada:
- Controle: não recebe qualquer tipo de intervenção.
- Meditação: participa de uma meditação de atenção plena (mindfulness) de 10 minutos.
- Música: Eescuta sons ambientais e música instrumental suave por 10 minutos.
Após a intervenção, ela aplica uma escala de estresse percebido nos estudantes universitários. Um exemplo de dados dessa pesquisa são apresentados na Figura 3.
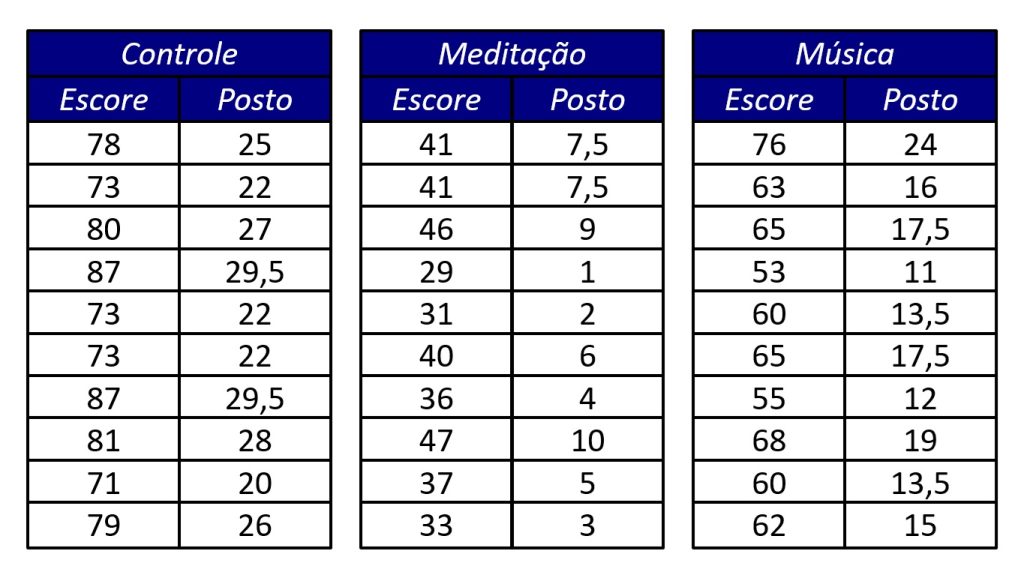
A ANOVA de uma via é aplicada à coluna Escore da Figura 3, enquanto o teste de Kruskal-Wallis transforma os escores em postos — inicialmente ignorando de qual grupo cada escore vem — e, em seguida, compara os postos entre os grupos.
A lógica do teste de Kruskal-Wallis é simples: se os grupos não diferirem entre si, esperaríamos os grupos igualmente espalhados ao longo dos postos (e médias dos postos aproximadamente iguais).
Em contrapartida, se há diferenças entre os grupos, os valores das somas dos postos deverão diferir. Desse modo, o teste de Kruskal-Wallis:
- Calcula os postos dos escores dos k grupos;
- Soma os postos de cada grupo;
- Calcula a estatística H, que avalia o quanto as médias de postos diferem entre os grupos.
Não mostraremos a fórmula da estatística H aqui, pois nosso foco é que você compreenda conceitualmente o teste. Mais importante que isso é que você saiba que softwares estatísticos transformam o H em um escore z, que tem um valor de p a ele associado. Esse valor de p indica quão prováveis são os dados, ou dados mais extremos, considerando a hipótese nula verdadeira.
Quais são as hipóteses nula e alternativa do teste de Kruskal-Wallis?
As hipóteses nula e alternativa do teste H de Kruskal-Wallis são as seguintes:
- Hipótese nula (H0): as amostras independentes dos k grupos têm a mesma tendência central e, portanto, são oriundas de uma mesma população.
- Hipótese alternativa (H1): pelo menos uma amostra independente não tem a mesma tendência central que as demais amostras e, portanto, é oriunda de uma população distinta.
Tal como ocorre em outros testes estatísticos, nós definimos um nível de significância (α) e realizamos nossa análise estatística. No caso do teste H de Kruskal-Wallis, obteremos uma estatística H, um escore z e um valor de p a ele associado. Se p < α, rejeitamos a hipótese nula.
Em outras palavras, considerando nosso exemplo, se p < α, assumimos que pelo menos um dos três grupos difere dos demais.
O teste post hoc de Dunn
O teste de Kruskal-Wallis examina se pelo menos um dos grupos difere estatisticamente dos demais. No entanto, assim como ocorre com a ANOVA de uma via, ele não indica quais grupos diferem entre si.
Para avaliarmos as diferenças par a par, utilizamos o teste de post hoc de Dunn. Em síntese, esse teste calcula a diferençe entre médias dos postos dos grupos de interesse e divide esse valor por uma estimativa do erro padrão dessa diferença.
Com base na estatística do teste, obtemos um valor de p, que é comparado com nosso nível de significância de interesse, de modo a avaliarmos se as diferenças entre pares de grupos são ou não estatisticamente significativas.
O teste de Kruskal-Wallis compara medianas?
É comum que se afirme que testes não paramétricos — incluindo o teste de Kruskal-Wallis — comparam medianas. No entanto, essa afirmativa é conceitualmente incorreta.
Embora não tenhamos apresentado a fórmula da estatística H de Kruskal-Wallis, ela nem sequer contém as medianas dos grupos. Pelo contrário, o que ela contém são os postos médios. Sendo assim, o teste de Kruskal-Wallis usa mais informações do que simplesmente as medianas dos grupos.
Como reportar os resultados de um teste de Kruskal-Wallis?
Os dados da Figura 3 são apresentados graficamente na Figura 4. Os boxplots parecem sugerir que os níveis de estresse percebido reduziram nos grupos experimentais (meditação e música), quando comparados ao grupo controle. Além disso, parece que a redução foi maior no grupo meditação.
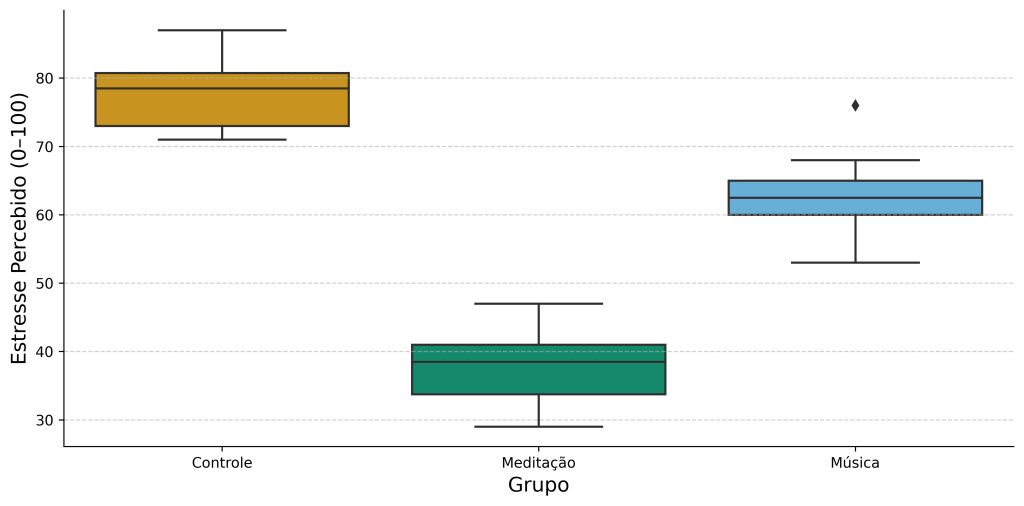
No entanto, a Figura 4 apresenta a variável dependente original, enquanto o teste de Kruskal-Wallis examina uma transformação dessa variável. A Figura 5 apresenta a saída da análise do teste de Kruskal-Wallis no SPSS.
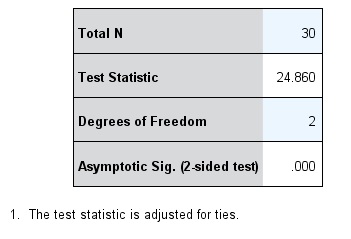
A estatística H é comparada com uma distribuição de qui-quadrado a fim de obter o valor de p que, em nosso exemplo, foi menor que 0,05. Sendo assim, assumimos que temos diferenças entre os grupos.
Mas quais grupos diferem entre si? A Figura 6 apresenta a comparação em pares. Note que, na coluna Sig., todas as comparações parecem ter atingido significância estatística. No entanto, após corrigirmos os valores ps para comparações múltiplas, apenas o grupo meditação diferiu estatisticamente dos demais grupos.
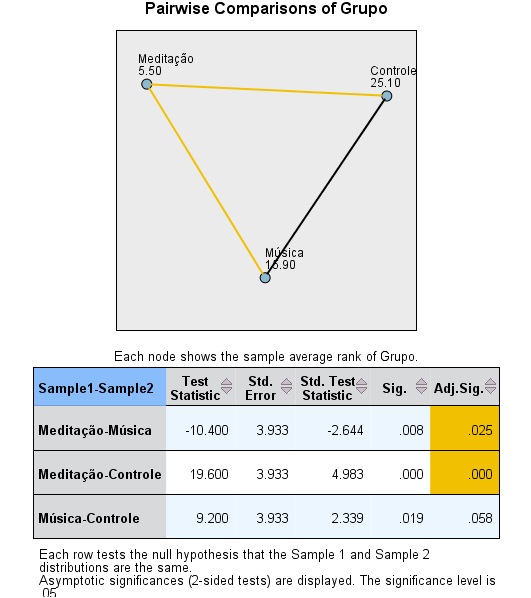
Com base nas informações acima, poderíamos descrever os resultados do teste de Kruskal-Wallis da seguinte maneira:
O estresse percebido dos estudantes universitários foi mais elevado no grupo controle (Mdn = 78,5, amplitude = 71–87, n = 10) e mais baixo no grupo meditação (Mdn = 38,5, amplitude = 29–47, n = 10); por fim, no grupo música, o estresse teve nível intermediário (Mdn = 62,5, amplitude = 53–76, n = 10). O teste de Kruskal-Wallis indicou diferenças significativas entre grupos, H(2) = 24,86, p < 0,001.
Comparações em pares (teste post hoc de Dunn) indicaram que a meditação reduziu significativamente os escores de estresse em comparação aos grupos controle, z = 4,98, p < 0,001, e música, z = –2,64, p = 0,025. Em contrapartida, a comparação entre os grupos música e controle não atingiram os níveis convencionais de significância, z = 2,34, p = 0,058.
Conclusão
Neste post, você aprendeu mais sobre o teste de Kruskal-Wallis, o equivalente não paramétrico da ANOVA de uma via. Gostou desse conteúdo? Então aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Academic press.
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Scheff, S. W. (2016). Nonparametric statistics. In S. W. Scheff (Ed.), Fundamental statistical principles for the neurobiologist : A survival guide (pp. 157–182). Elsevier. https://doi.org/10.1016/B978-0-12-804753-8.00008-7
Como citar este post
Lima, M. (2025, 11 de abril). O que é e quando usar o teste de Kruskal-Wallis? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/teste-de-kruskal-wallis/














