Quando usamos a análise de variância (ANOVA) em nossos estudos, precisamos acatar uma série de pressupostos estatísticos, de modo que possamos confiar nos resultados obtidos no teste. No entanto, isso nem sempre acontece. Sendo assim, neste post, iremos te ensinar a lidar, de modo metodologicamente adequado, com os pressupostos da análise de variância (ANOVA), quando eles não são acatados.
O que é análise de variância?
A análise de variância (ANOVA) é uma técnica estatística utilizada a fim de determinar se existem diferenças significativas entre as médias de três ou mais grupos independentes. No entanto, a validade das conclusões extraídas da ANOVA depende do rigoroso cumprimento de seus pressupostos: independência das observações, homogeneidade das variâncias e normalidade das distribuições dos grupos.

Como lidar quando os pressupostos da análise de variância não são atendidos?
Quando ocorre a violação de um ou mais pressupostos da ANOVA, os pesquisadores precisam adotar estratégias alternativas. Nesse sentido, é essencial escolher métodos que garantam análises estatísticas robustas. Além disso, essas abordagens devem preservar tanto a integridade dos dados quanto a correta interpretação dos resultados.
Contornando violações do pressuposto de independência das observações
Aqui trata-se de uma questão metodológica: a independência das observações pressupõe que o escore de um participante não influencia o escore de outro, ou seja, que os valores de cada participante do estudo seja independente e não influenciado pelos escores de outro participante.
Por exemplo, em um estudo na área de Educação, teremos violado esse pressuposto se amostrarmos estudantes de uma mesma turma (Figura 1). Isso ocorre porque estudantes de uma mesma turma são mais prováveis de compartilharem variáveis comuns (e.g., mesmo professor, mesma didática, mesmos passeios acadêmicos) que, consequentemente, podem influenciar variáveis de nossos estudos.

O pressuposto de independência deve ser considerado na fase de planejamento da coleta de dados. Caso o estudo explicitamente viole esse pressuposto, será necessário utilizar outras técnicas estatísticas, como os chamados modelos lineares generalizados hierárquicos, também conhecidos como modelos lineares mistos.
Contornando violações do pressuposto da distribuição de normalidade
O pressuposto de normalidade afirma que os escores dos participantes têm distribuição aproximadamente normal dentro de cada um dos grupos. A Figura 2 ilustra duas representações gráficas mostrando três grupos cujos escores não estão normalmente distribuídos (note as assimetrias nos boxplots, com destaque para o Grupo B).
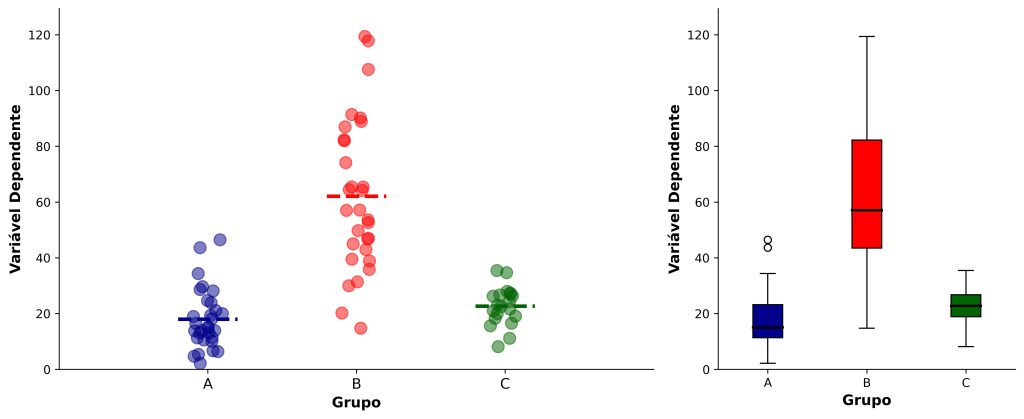
A literatura, em geral, vai recomendar duas formas para você lidar com a ausência da distribuição normal: o uso de testes não paramétricos ou a transformação logarítimica dos dados.
A problemática da transformação logarítmica
Embora a transformação logarítmica seja frequentemente sugerida como uma solução para a falta de normalidade ou homogeneidade das variâncias, ela pode não ser a panaceia esperada. Uma crítica central a essa abordagem é que raramente alcança a transformação dos dados em uma distribuição normal perfeita.
Além disso, essa transformação altera a escala original das variáveis, dificultando, portanto, a interpretação dos resultados (Feng et al., 2014). Sendo assim, é imperativo explorar alternativas que mantenham a integridade interpretativa dos dados.
A dificuldade com os testes não paramétricos
Se você estiver realizando uma ANOVA simples, então uma alternativa seria recorrer ao teste não paramétrico equivalente, que, nesse caso, é o teste de Kruskal-Wallis.
Embora o teste de Kruskal-Wallis seja metodologicamente adequado, é importante destacar que ele não utiliza a métrica original da variável de interesse.
Pelo contrário, esse teste transforma os escores originais em postos ordenados. Como resultado, a interpretação dos resultados se torna mais complexa, o que pode dificultar a análise dos dados.
Alternativas para lidar com violações do pressuposto de normalidade
Por isso, aqui iremos recomendar duas alternativas, que possibilitarão você realizar as suas análises com as métricas originais do seu banco de dados, mesmo que você não tenha distribuição normal.
1. Abordagem de bootstrapping: para dados que violam a pressuposição de normalidade, o bootstrapping emerge como uma técnica poderosa. Em síntese, por meio da reamostragem com reposição, cria-se uma distribuição de amostras que permite uma inferência estatística mais flexível e menos dependente de pressupostos rigorosos.
2. Modelos lineares generalizados (GLMs): os GLMs expandem os modelos lineares para incluir variáveis de resposta que não seguem uma distribuição normal. Para isso, eles utilizam funções de ligação que permitem modelar de forma mais precisa a relação entre as variáveis preditoras e a variável resposta. Dessa maneira, esses modelos oferecem uma abordagem versátil, especialmente quando os dados não atendem aos pressupostos tradicionais da ANOVA.
Lidando com a ausência de homogeneidade das variâncias
O pressuposto de homogeneidade das variâncias afirma que a variabilidade das observações dentro de cada um dos grupos é aproximadamente igual. A Figura 3 ilustra duas representações gráficas mostrando três grupos com variâncias heterogêneas: a variabilidade nos dados aumenta do Grupo A para o Grupo B e, novamente, do Grupo B para o Grupo C.
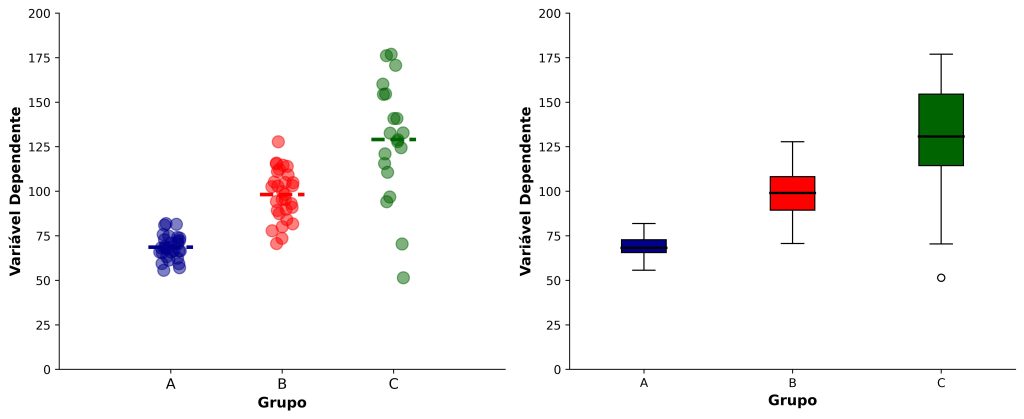
Se você se deparar com um cenário de heteroscedasticidade (ou seja, variâncias desiguais entre os grupos), não precisa se preocupar. Felizmente, a ANOVA conta com correções bem estabelecidas para lidar com essa questão, garantindo análises mais confiáveis.
1. Correção de Welch para ANOVA: quando a homogeneidade das variâncias é violada, a correção de Welch se apresenta como uma solução robusta. Essa abordagem ajusta os graus de liberdade da ANOVA com base nas variações dos tamanhos das amostras e suas respectivas variâncias. Como resultado, a análise se torna mais precisa, mesmo em condições de heteroscedasticidade.
2. Teste post hoc de Games-Howell: caso a correção de Welch indique diferenças significativas entre os grupos, podemos usar o teste post hoc de Games-Howell para avaliar quais grupos se diferenciam entre si. Além disso, esse teste não assume homogeneidade das variâncias, o que o torna uma opção mais adequada para dados que violam esse pressuposto.
Resumo: como lidar com violações aos pressupostos da análise de variância
Em síntese, sugerimos as seguintes correções:
a. Para ausência de normalidade: bootstrapping ou modelos lineares generalizados;
b. Para heterogeneidade de variâncias: correção de Welch para a ANOVA geral e post hoc de Games-Howell para as comparações em pares.
Se quiser ter acesso a esse conteúdo em formato de vídeo, assista abaixo:
Conclusão
Ao lidar com violações dos pressupostos da ANOVA, é essencial buscar alternativas metodológicas que não somente contornem essas limitações, mas que também preservem a clareza e a relevância da interpretação dos dados.
As estratégias discutidas — incluindo a correção de Welch, o teste de Games-Howell, o bootstrapping e os GLMs — oferecem caminhos promissores para análises robustas em face da não conformidade com os pressupostos tradicionais. A adoção dessas técnicas permite aos pesquisadores conduzir investigações rigorosas e interpretar seus resultados com confiança, mesmo na presença de dados complexos e desafiadores.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Feng, C., Wang, H., Lu, N., Chen, T., He, H., Lu, Y., & Tu, X. M. (2014). Log-transformation and its implication for data analysis. Shanghai Archives of Psychiatry, 26(2), 105–109. https://doi.org/10.3969/j.issn.1002-0829.2014.02.009
Como citar este post
Damásio, B. (2024, 6 de abril). Como lidar com os pressupostos da análise de variância (ANOVA)? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/pressupostos-da-analise-de-variancia-anova/














