Neste post, explicaremos o que é a correlação posto-bisserial. Além disso, diferenciaremos essa correlação de outra medida, de nome parecido, mas com uso distinto (a correlação ponto-bisserial). Por fim, por meio de dois exemplos, mostraremos como é fácil interpretar a correlação posto-bisserial, quer em delineamentos de grupos independentes, quer em delineamentos de medidas repetidas.
Postos das variáveis e os testes não paramétricos
Antes de mais nada, precisamos entender o conceito de postos. Em síntese, os postos são uma transformação da variável original, onde substituimos os escores originais por valores que indicam suas posições relativas na sequência ascendente de escores.
Por exemplo, suponha que temos os escores 8, 5, 19, 2 e 5. Podemos ordená-los em sequência ascendente e, em seguida, atribuíremos o valor 1 ao menor escore, o valor 2 ao segundo menor, e assim por diante. Desse modo, teremos a transformação representada na Figura 1.

Como temos dois escores iguais a 5, ao invés de atribuirmos os postos 2 e 3 a eles, nós calculamos a média desses postos, isto é, (2 + 3) / 2 = 2,5, e atribuímos esse mesmo valor a ambos os escores empatados.
Explicado o conceito de postos, podemos definir os testes não paramétricos. Resumidamente, os testes não paramétricos são métodos estatísticos que fazem suposições mínimas acerca das características das distribuições das variáveis.
Por exemplo, enquanto o teste t para amostras dependentes assume que a distribuição das diferenças é normal, seu equivalente não paramétrico (teste dos postos sinalizados de Wilcoxon) assume que essa distribuição é simétrica ao redor de um valor central.
Os testes não paramétricos comumente utilizam os postos em suas análises. Desse modo, enquanto um teste paramétrico usaria os números da linha Escores, na Figura 1, um teste não paramétrico transformaria esses valores na linha Postos, e faria seus cálculos nessa transformação da variável original.
Para concluir, note que, embora os postos modifiquem os valores da variável original, eles preservam o ranqueamento relativo dos casos. Em outras palavras, o menor escore original seguirá sendo o menor escore, quando considerarmos seu posto, sendo que o mesmo ocorrerá para os demais escores.

A correlação posto-bisserial
A correlação posto-bisserial (rank-biserial correlation, rrb) quantifica a força e a direção da relação entre uma variável dicotômica e uma variável ordinal (e.g., os postos). Note que ela é diferente da correlação ponto-bisserial (rpb), que mensura a força e a direção da relação entre uma variável dicotômica e uma variável contínua.
Por exemplo, para quantificarmos a força da relação entre status de fumante (fuma, não fuma) e níveis de colesterol, podemos usar a correlação ponto-bisserial.
No entanto, suponha que os níveis de colestesterol tenham forte assimetria em nossa amostra, de modo que preferimos analisar os efeitos do status do fumante sobre os níveis de colesterol por meio do teste de Mann-Whitney, o equivalente não paramétrico do teste t para amostras independentes. Nesse caso, podemos usar a correlação posto-bisserial para estimar o tamanho de efeito em nossos dados.
Intuição por trás da correlação posto-bisserial
Kerby (2014) introduziu uma maneira didática de entender a correlação posto-bisserial. Assuma que queremos avaliar o efeito de uma intervenção sobre o tempo que atletas levam para concluir uma corrida. Cinco atletas foram aleatoriamente designados ao grupo intervenção, e quatro, ao grupo controle.
A Figura 2 apresenta o tempo (em segundos) que cada atleta levou para realizar a corrida. Nossa expectativa é que a intervenção melhoraria o desempenho dos atletas, o que se refletiria em menores tempos para realizar a corrida.
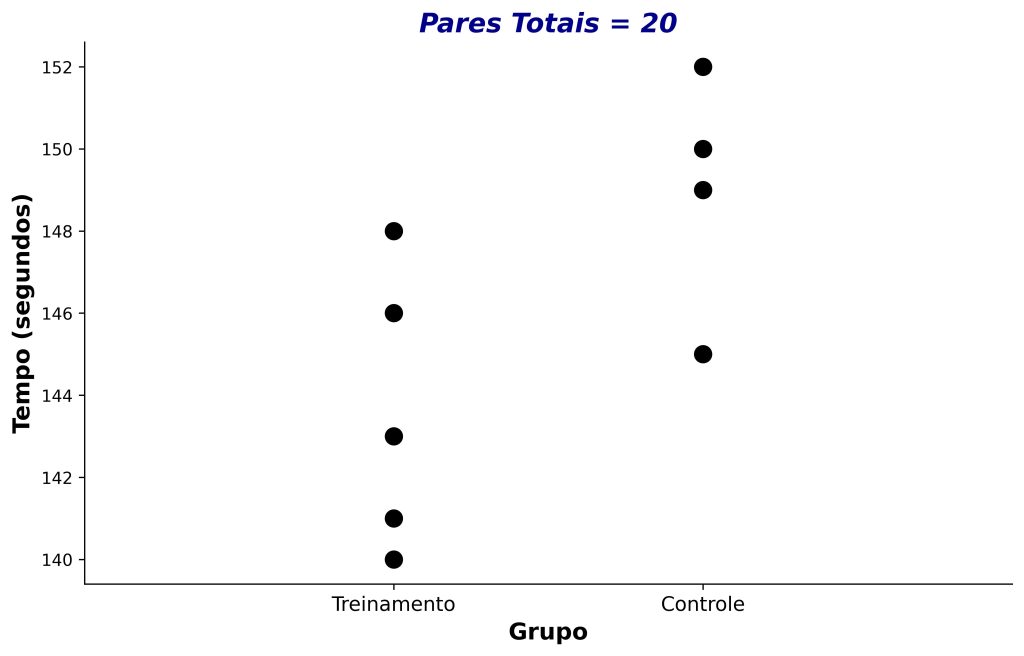
Na Figura 2, os pares totais refletem o número de maneiras que podemos formar pares de atletas, sendo um de cada grupo. O número de pares é obtido pelo produto do número de participantes em cada grupo, isto é, 5 × 4 = 20 pares totais.
A Figura 3 apresenta os dados anteriores, mas agora destacando os pares favoráveis, isto é, aqueles que apoiam nossa hipótese de pesquisa. Em outras palavras, representamos, por meio de linhas cinzas, os pares em que o tempo foi menor para o atleta do grupo intervenção, em comparação ao do atleta do grupo controle. Note que, nos pares favoráveis, todas as retas têm inclinação positiva.
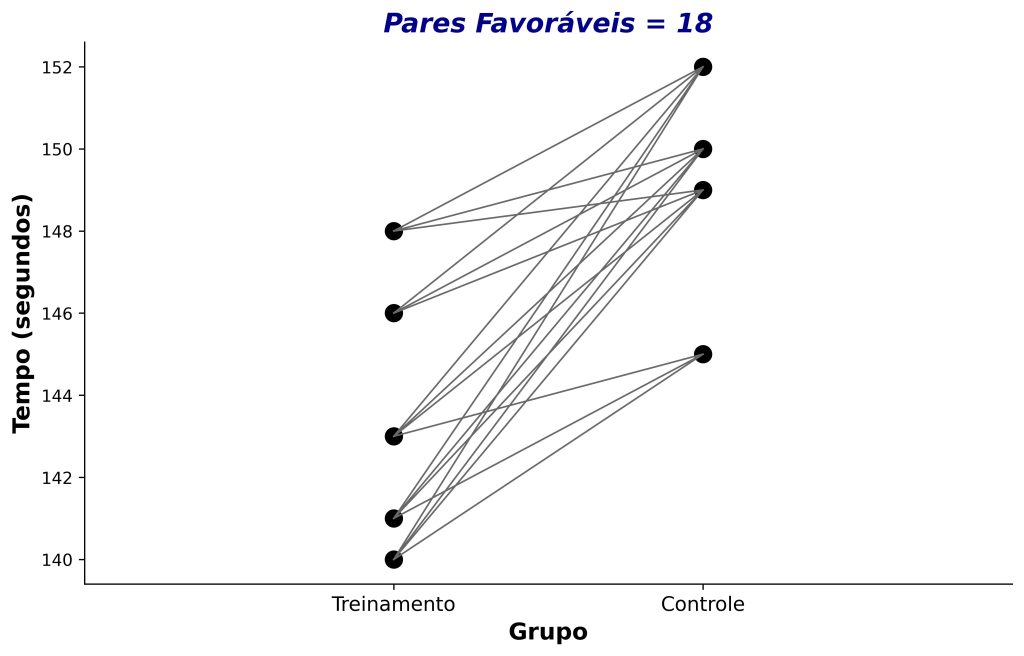
Já a Figura 4 destaca os pares desfavoráveis, que são aqueles que não apoiam nossa hipótese. Existem apenas dois pares desfavoráveis, pois há apenas um participante do grupo controle com tempo inferior a dois atletas do grupo intervenção. Nos pares desfavoráveis, as retas têm inclinação negativa.
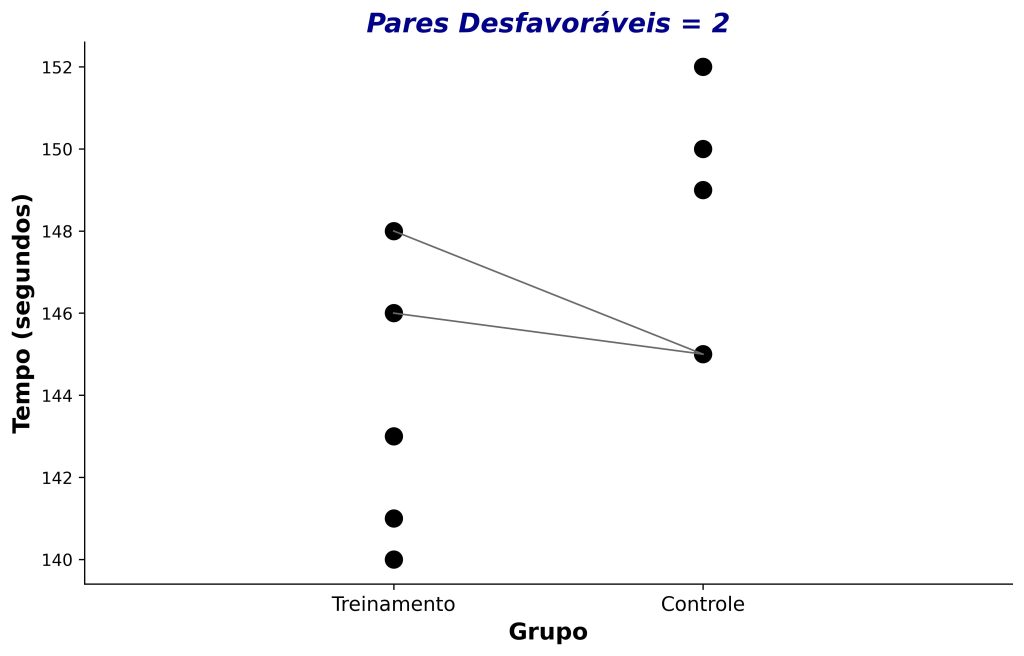
Como veremos a seguir, uma maneira simples e intuitiva de compreender a correlação posto-bisserial é como um índice que quantifica a evidência favorável versus desfavorável à nossa hipótese.
Como interpretar a correlação posto-bisserial no teste de Mann-Whitney?
Lembrando, os dados do exemplo da corrida poderiam ser analisados por meio do teste de Mann-Whitney, onde comparamos o tempo de corrida em função dos grupos (intervenção vs. controle). Embora não seja nosso intuito mostrar como realizar essa análise aqui, apresentamos, na Figura 5, a saída dos testes t para amostras independentes e de Mann-Whitney no JASP. Note que rrb = 0,80.
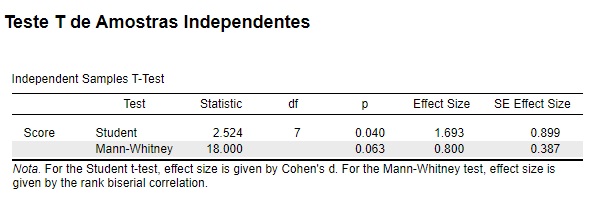
Mas como esse valor deve ser interpretado? Para compreendermos sua interpretação, retomaremos as ideias de pares favoráveis e desfavoráveis que introduzimos anteriormente. A correlação posto-bisserial consiste na diferença entre a proporção de pares favoráveis e de pares desfavoráveis. Desse modo, como tivemos 18 de 20 casos favoráveis e 2 de 20 casos desfavoráveis, temos:
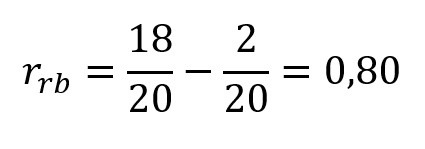
O que leva a um resultado idêntico ao obtido no JASP. Desse modo, podemos interpretar esse coeficiente como indicando que a evidência para um efeito do treinamento sobre o tempo para realizar a corrida foi forte e na direção que hipotetizamos.
Por fim, é relevante notar que, caso tivéssemos os mesmos dados, mas nossa hipótese fosse na direção oposta, a subtração teria sido feita na direção contrária, o que resultaria em um rrb = –0,80. Se esse tivesse sido o caso, a força da correlação ainda seria forte, mas expressaria que o efeito da intervenção foi na direção contrária ao que esperávamos.
Como interpretar a correlação posto-bisserial no teste de Wilcoxon?
Suponha que aplicamos uma intervenção em um grupo de oito participantes, visando aumentar a felicidade marital deles. Nossa hipótese é de que a felicidade marital aumentaria do pré- para o pós-teste. A Figura 6 apresenta os dados dos participantes deste delineamento de medidas repetidas.
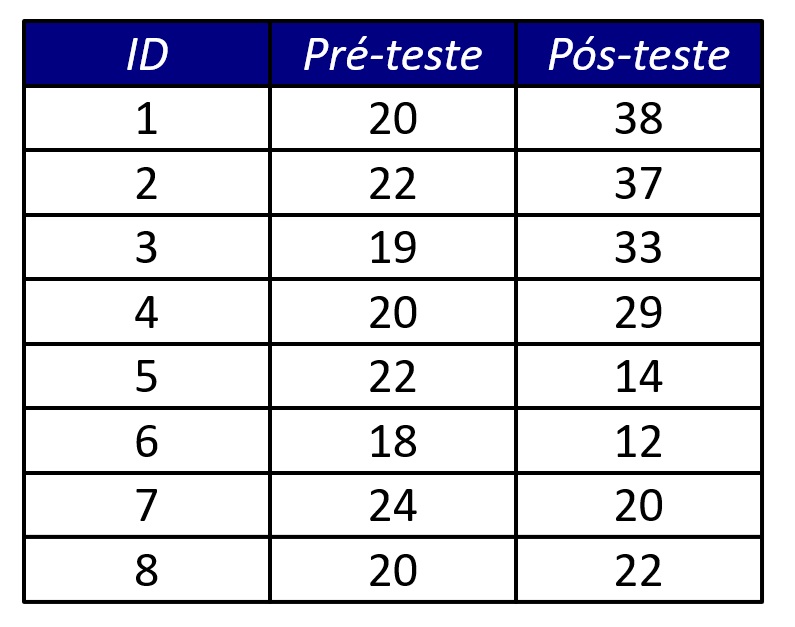
Em seguida, calcularemos a diferença entre variáveis, isto é, Δ = Pós-teste – Pré-teste. Valores positivos de Δ são favoráveis à nossa hipótese, pois, se Δ é positivo, isso quer dizer que a felicidade marital aumentou após a intervenção.
O teste t para amostras dependentes se baseia nos valores de Δ. Já o teste de Wilcoxon descarta valores nulos de Δ e calcula os postos dos módulos das diferenças, isto é, ignorando os sinais de Δ. Por fim, ele soma, separadamente, os postos associados às diferenças positivas e os postos associados às diferenças negativas. A Figura 7 mostra esses cálculos.
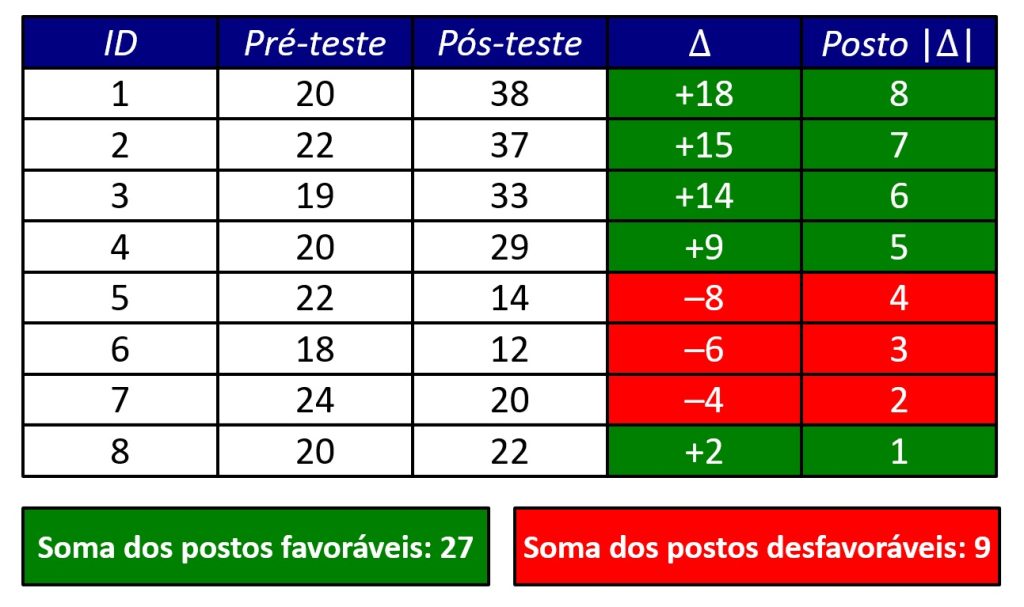
No caso do teste de Wilcoxon, a correlação posto-bisserial consiste na diferença entre a proporção de postos favoráveis e de postos desfavoráveis. Desse modo, como a soma dos postos favoráveis foi 27, a dos postos desfavoráveis foi 9 e o total foi 36, temos:
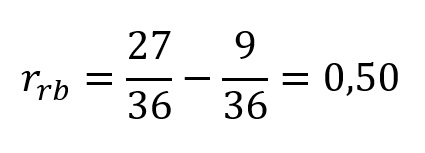
O que é exatamente igual ao resultado que obtivemos no JASP com esses mesmos dados (Figura 8).
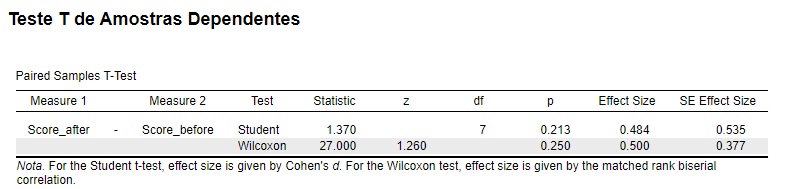
Assim como no exemplo anterior, podemos interpretar o rrb = 0,50 como um efeito forte, indicando que a intervenção de fato teve uma correlação com os escores de felicidade marital na direção que esperávamos.
Conclusão
Neste post, você aprendeu o que é e como interpretar o coeficiente de correlação posto-bisserial. Além disso, você aprendeu a diferença entre ele e o coeficiente de correlação ponto-bisserial que, embora tenha nome parecido, se aplica a casos quando uma das variáveis é contínua (e não ordinal).
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Kerby, D. S. (2014). The simple difference formula: An approach to teaching nonparametric correlation. Innovative
Teaching, 3, Article 1. https://doi.org/10.2466/11.IT.3.1
Como citar este post
Lima, M. (2025, 15 de janeiro). O que é correlação posto-bisserial? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-correlacao-posto-bisserial














