Durante a avaliação das propriedades psicométricas de instrumentos psicológicos, pesquisadores comumente precisam decidir o número de fatores a extrair a partir do banco de dados. Neste post, falaremos sobre um dos critérios de decisão do número de fatores, a saber, a análise paralela.
Qual é a importância de decidir quantos fatores reter na análise fatorial?
O objetivo da análise fatorial exploratória é explicar, por meio de um número menor de fatores, a maior parte da variância comum observada nas variáveis originais. Desse modo, pesquisadores precisam decidir o número de fatores a extrair, de modo a obter soluções fatoriais parcimoniosas, com plausibilidade teórica e, ao mesmo tempo, com bom poder explicativo.
Neste sentido, a decisão sobre o número correto de fatores é essencial, pois ela afeta diretamente a interpretabilidade dos resultados, bem como a teorização na área. Por exemplo, considere que a estrutura verdadeira dos traços de personalidade seria representada por cinco grandes fatores. Sendo assim, dois erros que gostaríamos de evitar são:
- A superestimação de fatores, isto é, a retenção incorreta de seis ou mais fatores;
- A subestimação de fatores, isto é, a retenção incorreta de quatro ou menos fatores.
Na prática, contudo, deparamo-nos com um problema: não temos como saber se estamos superestimando ou subestimando o número de fatores, pois isso exigiria conhecermos o modelo “verdadeiro”. Mas, se soubéssemos qual é o modelo verdadeiro, não precisaríamos conduzir a pesquisa!
Felizmente, por meio de estudos de simulação, somos capazes de definir a estrutura latente correta, de amostrar dados fictícios e, desse modo, comparar o desempenho de diferentes critérios de decisão do número de fatores a reter. Em seguida, exploraremos um desses critérios.
Veja também: Quais são os principais métodos de retenção de fatores na análise fatorial exploratória?

Alguns conceitos de análise fatorial exploratória
Primeiramente, vamos revisar alguns conceitos. Na análise fatorial exploratória, podemos construir uma matriz de correlação entre as diferentes variáveis, com base nos dados brutos dos participantes — ou uma matriz de correlação reduzida, em que os elementos da diagonal principal contêm estimativas das comunalidades das variáveis.
Por exemplo, suponha que aplicamos nosso instrumento, contendo nove items (V1 a V9), em 200 respondentes. Com base nessas respostas, podemos obter a matriz de correlações entre as respostas aos itens (Figura 1).

Por meio de métodos da álgebra linear (i.e., eigendecomposition), a análise fatorial extrai eigenvalues (ou autovalores) e autovetores da matriz de correlações.
Aqui você não precisa se preocupar com a parte matemática, mas apenas com seu significado conceitual. Cada eigenvalue expressa a variância comum a um conjunto de variáveis do instrumento original. Um eigenvalue igual a 1 indica que um fator explica uma quantidade de variância equivalente à variância total de uma variável padronizada (com desvio-padrão igual a 1).
A análise fatorial exploratória gera um número de eigenvalues igual ao número de itens no instrumento original (em nosso exemplo da Figura 1, a análise fatorial exploratória produziria nove eigenvalues).
Idealmente, gostaríamos que um pequeno número de eingenvalues capturasse uma porção substancial da variância das variáveis originais. Por exemplo, se três eigenvalues possuem valores maiores, enquanto os demais possuem valores irrisórios, é possível que três fatores sejam capazes de explicar boa parte da variância em nosso banco de dados.

O que é análise paralela?
A análise paralela é um método de simulação Monte Carlo usado para decidir qual o número de fatores a extrair de um conjunto de dados.
Em síntese, na análise paralela, nós geramos matrizes de correlações aleatórias não correlacionadas, considerando os mesmos números de respondentes (n) e de itens (p) que os existentes em nosso banco de dados original.
Esse procedimento se repete centenas ou milhares de vezes. Em cada repetição, realizamos a decomposição de nossa matriz aleatória, extraindo os eigenvalues e guardando os valores obtidos. Por fim, nós obteremos uma distribuição amostral de eigenvalues aleatórios, a partir da qual podemos calcular os eigenvalues médios associados a cada fator (de 1 até p).
O objetivo é comparar nossos eigenvalues empíricos, isto é, aqueles obtidos em nossos dados reais, com os eigenvalues médios aleatórios, isto é, aqueles obtidos em nossa simulação Monte Carlo. Podemos pensar nos eigenvalues dos dados simulados como uma estimativa de valores que seriam esperados apenas devido a fatores aleatórios.
A lógica da análise paralela é comparar os eigenvalues dos dados reais com os eigenvalues dos dados simulados. Esperamos que nossos eigenvalues capturem mais variância real que um eigenvalue obtido por meio de matrizes aleatórias não correlacionadas.
Exemplo de análise paralela
Em seguida, daremos um exemplo de resultado da análise paralela. A fim de ilustrar o critério da análise paralela, a Figura 2 apresenta os eigenvalues obtidos a partir dos dados reais e a partir dos dados simulados pela simulação Monte Carlo.
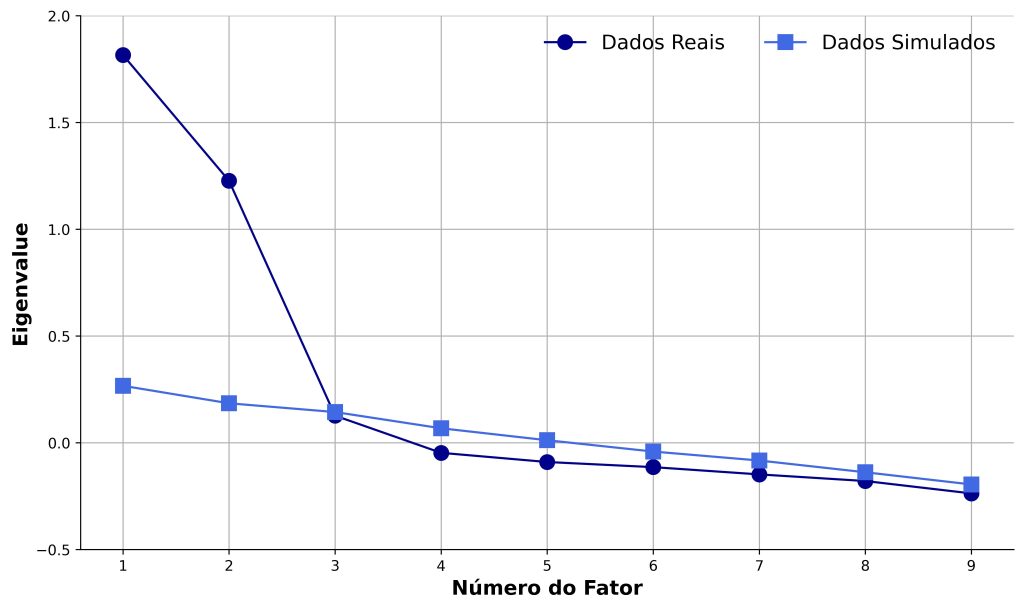
Primeiramente, comparamos o primeiro eigenvalue dos dados reais (1,816) com o primeiro eigenvalue dos dados simulados (0,267). Como o valor do eigenvalue empírico é maior, assumimos que o primeiro fator em nossos dados explica mais variância do que seria esperada considerando matrizes aleatórias não correlacionadas; portanto, esse provavelmente é um fator verdadeiro.
Em seguida, comparamos o segundo par de eigenvalues (dados reais: 1,227; dados simulados: 0,185). Mais uma vez, a variância explicada pelo segundo fator é maior do que o esperado pelo modelo aleatório. Repetimos esse procedimento até que o eigenvalue dos dados reais seja menor que 1 ou seja menor que o dos dados simulados — o que, na Figura 2, ocorre no terceiro fator. Desse modo, a análise paralela recomenda a extração de até dois fatores.
Note que, na Figura 2, o terceiro eigenvalue dos dados reais foi simultaneamente menor que 1 e menor que o dos dados simulados. No entanto, em algumas situações, um eigenvalue poderá ser maior que 1, mas menor que o dos dados simulados.
Em tais casos, o critério da análise paralela recomendará um número de fatores menor que o critério de Kaiser–Guttman (eigenvalue > 1) que, sabidamente, superestima o número de fatores em alguns cenários de estudos de simulação.
Procedimentos de análise paralela
Embora vários procedimentos recebam o nome de análise paralela, é importante frisar que há diferenças entre eles. Originalmente, Horn (1965) propôs a análise paralela para extração de componentes — e não de fatores —, no contexto da análise de componentes principais.
A análise paralela de Horn, diferente do que ilustramos anteriormente, usa 1s na diagonal principal da matriz de correlação, consistente com a ideia de que a análise de componentes principais considera variâncias específicas e comum aos itens.
Em contrapartida, a implementação que descrevemos anteriormente é consistente com a análise fatorial exploratória, pois considera a matriz reduzida, que substitui os 1s na diagonal principal por estimativas das comunalidades. A abordagem que descrevemos é baseada na fatoração pelos eixos principais (parallel analysis based on principal axis factor analysis; PA-PAFA).
Por fim, os desenvolvedores do FACTOR propuseram um terceiro procedimento, baseado no posto mínimo (parallel analysis based on minimum rank factor analysis; PA-MRFA). No FACTOR, essa implementação é conhecida como implementação otimizada. Essa abordagem se baseia em variância comum explicada e em permutação aleatória dos dados amostrais, performando melhor que outros métodos em um estudo de simulação inicial (Timmerman & Lorenzo-Seva, 2011).
Onde realizar a análise paralela?
Pesquisadores têm diversas opções para realizar análises paralelas. Por exemplo, o software Monte Carlo PCA for Parallel Analysis implementa a técnica de Horn (1965), mas apresenta restrições quanto aos números máximos de respondentes, de itens e de iterações.
Outras opções acessíveis incluem o pacote psych, do R, o JASP e o FACTOR. Por exemplo, no caso do R, a análise paralela é facilmente implementada pelo código a seguir:
# importa pacote psych
library(psych)
# implementa análise
analise_paralela <- psych::fa.parallel(data, # dataframe contendo as respostas dos participantes aos itens
cor = "poly", # matriz de correlação policórica
fa = "fa", # análise fatorial
fm = "minrank" # método baseado no posto mínimo (MRFA)
)
Conclusão
Neste post, você aprendeu o que é análise paralela. Gostou desse conteúdo? Aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades!
Se você pecisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Bandalos, D. L. (2018). Measurement theory and applications for the social sciences. The Guilford Press.
Damásio, B. F. (2012). Uso da análise fatorial exploratória em psicologia. Avaliação Psicológica, 11(2), 213–228.
Horn, J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30, 179–185. https://doi.org/10.1007/BF02289447
Timmerman, M. E., & Lorenzo-Seva, U. (2011). Dimensionality assessment of ordered polytomous items with parallel analysis. Psychological Methods, 16(2), 209–220. https://doi.org/10.1037/a0023353
Como citar
Lima, M. (2024, 25 de dezembro). O que é análise paralela? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-analise-paralela/














