O que é análise fatorial exploratória?
A análise fatorial exploratória (AFE) é um conjunto de técnicas multivariadas usado a fim de identificar padrões subjacentes em um conjunto de dados. Em síntese, seu principal objetivo é descobrir fatores latentes — variáveis não observadas — que explicam as correlações entre as variáveis medidas (e.g., respostas aos itens de um instrumento de autorrelato).
Em vez de partir de hipóteses pré-definidas, a AFE busca revelar a estrutura dos dados. Ela se baseia em uma matriz de correlação ou covariância e estima quais fatores latentes melhor representam as relações entre as variáveis observadas.
O modelo teórico assume que cada variável observada é influenciada por um ou mais fatores latentes. Desse modo, o intuito da técnica é reduzir o número de variáveis, mantendo a maior parte da informação original. Assim, a técnica simplifica a estrutura dos dados e facilita sua interpretação.

Procedimentos estatísticos comumente utilizados ao realizar uma análise fatorial exploratória
Durante o processo, diversas decisões metodológicas são necessárias. Evidentemente, todas elas devem se apoiar em fundamentos teóricos e critérios estatísticos sólidos. Em seguida, apresentamos os principais procedimentos usados em cada etapa de uma AFE.
Procedimentos para avaliar a adequação da amostra
Antes de iniciar a AFE, é essencial verificar se os dados são adequados para essa técnica. Para esse fim, existem dois testes tipicamente utilizados:
1. Índice Kaiser-Meyer-Olkin (KMO): esse índice mede a adequação da amostra com base nas correlações entre as variáveis. Os valores de KMO variam de 0 a 1, sendo que valores acima de 0,70 indicam que a AFE é apropriada, enquanto valores abaixo de 0,50 são considerados inaceitáveis.
2. Teste de esfericidade de Bartlett: esse teste verifica se a matriz de correlação é significativamente diferente da matriz identidade. Relembrando, uma matriz identidade é uma matriz quadrada onde existem 1s na diagonal principal e 0s nas demais células (Figura 1).
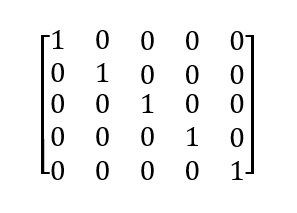
Se a matriz de correlação baseada em nossos dados não for significativamente diferente da matriz identidade com o mesmo número de variáveis que em nossos dados, então isso sugere que nossas variáveis têm correlações muito baixas — isto é, que a matriz de correlações não é fatorável.
Por outro lado, se o teste de esfericidade de Bartlett retorna um resultado estatisticamente significativo (p < 0,05), então temos evidência de que existe interdependência entre as variáveis, o que justifica a realização da AFE.
Procedimentos para retenção de fatores
Após garantir a adequação da amostra, é hora de decidir quantos fatores extrair. Em seguida, apresentamos os três métodos mais comuns para retenção fatorial:
1. Critério do autovalor > 1 (critério de Kaiser): a AFE extrai autovalores (eingevalues) da matriz de correlações, que expressam a variância comum a um conjunto de variáveis do instrumento original. Um autovalor igual a 1 indica que um fator explica uma quantidade de variância equivalente à variância total de uma variável padronizada (com desvio-padrão igual a 1).
Em síntese, o critério do autovalor > 1 sugere reter apenas fatores com autovalores maiores que 1. A ideia é que cada fator selecionado explique mais variância do que uma única variável observada.
2. Critério do gráfico de sedimentação (scree plot): proposto por Cattell (1966), esse gráfico mostra os autovalores em ordem decrescente, onde o ponto de inflexão da curva indica o número ideal de fatores a reter. Em outras palavras, buscamos reter o número de fatores igual ao ponto do scree plot onde ele forma um “cotovelo” (Figura 2).

3. Análise paralela: desenvolvida por Horn (1965), esse método compara os autovalores obtidos nos dados reais com autovalores gerados a partir de matrizes aleatórias. Apenas os fatores com autovalores superiores aos da matriz aleatória devem ser retidos.
Contudo, os critérios de Kaiser e scree plot tendem a superestimar o número de fatores. Por outro lado, a análise paralela costuma oferecer resultados mais precisos, especialmente com dados ordinais.
Saiba mais: O que é análise paralela?

Métodos de extração fatorial
Em seguida, devemos escolher o método para estimar as cargas fatoriais. Veja os mais utilizados na análise fatorial exploratória:
- Máxima verossimilhança (maximum likelihood, ML): requer normalidade multivariada e, portanto, pode não funcionar bem com amostras pequenas ou dados ordinais.
- Mínimos quadrados não ponderados (unweighted least squares, ULS): é mais robusto frente a violações da normalidade e adequado para variáveis ordinais.
- Mínimos quadrados ponderados diagonalmente (diagonally weighted least squares, DWLS): altamente recomendado para dados ordinais e amostras pequenas. Tem se mostrado o mais robusto entre os três.
Por fim, evite confundir AFE com análise de componentes principais (ACP). Esta última não visa encontrar fatores latentes, mas componentes que maximizam a variância total. Para mais detalhes, veja nosso post sobre a diferença entre AFE e ACP.
Veja também: Análise fatorial e análise de componentes principais: diferenças e quando usar

Rotação dos fatores
A rotação dos fatores facilita a interpretação dos resultados, pois ela distribui melhor as cargas fatoriais em seus fatores primários. Em síntese, existem duas famílias de rotação dos fatores:
- Rotação ortogonal: mantém os fatores independentes. Exemplo: varimax.
- Rotação oblíqua: embora não obrigue, ela permite correlação entre os fatores. Exemplo: oblimin. É a mais indicada na maioria das aplicações em ciências sociais.
Após a rotação, as variáveis se alinham de forma mais clara aos fatores, tornando assim os resultados mais compreensíveis.
Como interpretar uma análise fatorial exploratória?
Com os fatores extraídos e os dados rotacionados, chegou a hora de interpretar os resultados. Para isso, comece analisando as cargas fatoriais dos itens.
Em geral, cargas acima de 0,30 são geralmente consideradas significativas. No entanto, se você deseja uma estrutura mais rigorosa, pode usar um ponto de corte de 0,40.
Além dos valores numéricos, avalie também a coerência teórica dos fatores. Sendo assim, os itens que compõem um fator devem refletir uma dimensão comum. Por exemplo, em um questionário de personalidade, o fator “extroversão” deve reunir itens relacionados à sociabilidade e assertividade. Contudo, não basta que os dados mostrem agrupamentos, pois eles também precisam fazer sentido à luz da teoria.
Se você ainda se sente inseguro para interpretar uma análise fatorial exploratória, então assista ao nosso tutorial no YouTube: “Como fazer a análise fatorial exploratória perfeita”.
Conclusão
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cattell, R. B. (1966). The scree test for the number of factors. Multivariate Behavioral Research, 1(2), 245–276. https://doi.org/10.1207/s15327906mbr0102_10
Horn, J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30(2), 179–185. https://doi.org/10.1007/BF02289447
Como citar este post
França, A. (2025, 7 de maio). Análise fatorial exploratória: O que é, para que serve e os principais procedimentos. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/analise-fatorial-exploratoria-o-que-e-para-que-serve-e-como-e-realizada/














