Neste post, falaremos sobre a variância média extraída, um indicador da fidedignidade dos escores de um instrumento. Primeiramente, definiremos o indicador e apresentaremos sua fórmula. Em seguida, relacionaremos a variância média extraída com o conceito de fidedignidade da teoria clássica dos testes. Por fim, nós apresentaremos um exemplo detalhado de como usar as informações fornecidas por uma análise fatorial confirmatória para computar as variâncias médias extraídas dos fatores do modelo.
O que é variância média extraída?
A variância média extraída (VME) — ou average variance extracted (AVE) — é um indicador estatístico utilizado principalmente na validação de construtos latentes em modelos de mensuração.
Introduzida por Fornell e Larcker (1981), a VME mede a proporção de variância capturada por um construto em relação à variância atribuída ao erro de mensuração. Ou seja, ela indica o quanto os indicadores realmente refletem o construto que deveriam medir.
A VME é fundamental para avaliar a fidedignidade dos escores. Quanto maior a VME, mais confiança temos de que os indicadores estão captando bem o construto latente subjacente.

Qual é a fórmula da variância média extraída?
Em seguida, introduzimos a fórmula da VME (Fornell & Larcker, 1981, Equação 11; Valentini & Damásio, 2016, Equação 3):
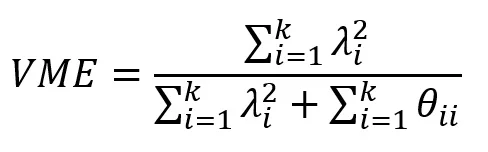
onde λi é a carga fatorial padronizada do item i, θii é a variância residual do item i, e k é o total de itens em um fator.
Em outras palavras, somamos os quadrados das cargas fatoriais e dividimos o valor obtido pela soma dos quadrados das cargas mais a soma das variâncias residuais.
Uma maneira intuitiva — e matematicamente equivalente — de pensar na fórmula anterior é considerando que, tipicamente, temos a seguinte relação entre as cargas fatoriais padronizadas e as variâncias residuais de uma análise fatorial confirmatória: λi2 + θii = 1 (note que esse é exatamente o termo de uma iteração do denominador da fórmula da VME).
Uma vez que nossa variável indexadora i vai de 1 até k, o denominador resultará no próprio valor de k — o número de indicadores carregando em um dado fator na análise fatorial confirmatória. Sendo assim, a fórmula a seguir é conceitualmente equivalente à anterior (Valentini & Damásio, 2016, Equação 4):

Em outras palavras, essa fórmula deixa explícito que a VME consiste na média dos quadrados das cargas fatoriais padronizadas — o que é totalmente consistente com a expressão variância média extraída.
O valor da VME varia entre 0 e 1. Um valor acima de 0,50 é geralmente considerado aceitável, pois indica que mais da metade da variância dos indicadores é explicada pela variável latente e que as cargas fatoriais são, em média, 0,70 (Valentini & Damásio, 2016).
Como o conceito de variância média extraída se relaciona com a teoria clássica dos testes?
Embora Fornell e Larcker (1981) argumentem que a variância média extraída é uma medida de validade convergente, Valentini e Damásio (2016) contra-argumentam, de forma convincente, que ela é, na verdade, um índice de fidedignidade — que eles chamam de precisão no artigo original.
A teoria clássica dos testes (TCT) propõe que o escore observado (X) é a soma do escore verdadeiro (T) e um erro de mensuração (E). Desse modo, no contexto da TCT, a fidedignidade dos escores é definida como a proporção da variância nos escores observados que consistem em escores verdadeiros. Formalmente, temos a seguinte representação conceitual (Bandalos, 2018):
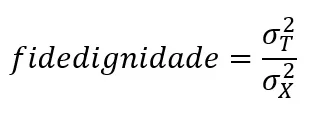
onde σ2T se refere à variância do escore verdadeiro e σ2X, à variância do escore observado. Uma vez que σ2X = σ2T + σ2E, onde σ2E se refere à variância residual, a conceitualização acima pode ser reexpressa da seguinte maneira:

Logo, quanto menor a variância residual (σ2E), maior a fidedignidade dos escores. Sendo assim, a VME se alinha com os princípios da TCT, ao distinguir a variância que é atribuída à variável latente daquela causada por erro de mensuração.
Desse modo, a VME mostra diretamente a quantidade de variância explicada pelo fator relativa à quantidade de variância decorrente de erro de medida — o que ajuda a validar a estrutura fatorial dos instrumentos (i.e., validade baseada na estrutura interna).
Portanto, a VME complementa as análises clássicas de fidedignidade, oferecendo uma perspectiva mais robusta sobre a qualidade psicométrica de um conjunto de itens.
Exemplo de cálculo da variância média extraída
O banco de dados
Unsworth et al. (2005) administraram três tarefas de capacidade de memória de trabalho (operation span, automated operation span e reading span) e duas tarefas de inteligência fluida (matrizes avançadas progressivas de Raven [Raven] e rotated blocks) a 296 participantes.
Infelizmente, os autores não disponibilizaram publicamente os dados da pesquisa, nem apresentaram a matriz de correlações de todas as medidas para o banco de dados completo. No entanto, em uma etapa de teste–reteste da pesquisa, eles apresentaram a matriz de correlações para uma subamostra de 78 participantes (Tabela 1).

Em seguida, usaremos os valores da Tabela 1 para demonstrar o cálculo da variância média extraída. Contudo, vale salientar que, uma vez que a matriz de correlações da Tabela 1 não representa os dados completos, nossas análises reproduzem apenas aproximadamente os resultados reportados por Unsworth et al. (2005).
Ajuste de modelo aos dados usando análise fatorial confirmatória
A fim de obtermos os valores necessários para o cálculo da variância média extraída, é necessário ajustarmos um modelo de análise fatorial confirmatória aos dados, de modo a obtermos as cargas fatoriais padronizadas e as variâncias residuais.
Para isso, usaremos o pacote lavaan, do R. Primeiramente, carregaremos o pacote, criaremos um objeto do tipo matrix para armazenar nossa matriz de correlações e definiremos nosso tamanho amostral.
# Instala e carrega o lavaan
install.packages("lavaan")
library(lavaan)
# Define a matriz de correlação
# e o tamanho da amostra
unsworth <- matrix(c(
1.000, 0.499, 0.453, 0.710, 0.411, 0.306,
0.499, 1.000, 0.831, 0.603, 0.363, 0.224,
0.453, 0.831, 1.000, 0.627, 0.387, 0.264,
0.710, 0.603, 0.627, 1.000, 0.403, 0.147,
0.411, 0.363, 0.397, 0.403, 1.000, 0.387,
0.306, 0.224, 0.264, 0.147, 0.387, 1.000
),
nrow = 6,
byrow = TRUE,
dimnames = list(c("ospan", "aospan", "retest_aospan",
"rspan", "raven", "rotated_blocks"),
c("ospan", "aospan", "retest_aospan",
"rspan", "raven", "rotated_blocks")))
)
# Define o tamanho da amostra
# (similar a Unsworth et al., 2005)
sample_size <- 78
Em seguida, definiremos nosso modelo de análise fatorial confirmatória. O operador =~ especifica as variáveis observadas ospan, aospan e rspan para a variável latente memoria_de_trabalho, bem como as variáveis observadas raven e rotated_blocks para a variável latente inteligencia_fluida.
# Definir o modelo de AFC
model <- '
memoria_de_trabalho =~ ospan + aospan + rspan
inteligencia_fluida =~ raven + rotated_blocks
'
Por fim, ajustamos nosso modelo aos dados.
# Ajustar o modelo aos dados
fit <- cfa(model,
sample.cov = unsworth,
sample.nobs = sample_size)
Calculando a variância média extraída de cada fator
Para consultar as saídas, executamos o código a seguir.
# Verifica os resultados
summary(fit, fit.measures = TRUE, standardized = TRUE)
A Figura 1 apresenta trechos selecionados da saída do código anterior. Indicamos onde, nessa saída, aparecem as cargas fatoriais padronizadas e as variâncias residuais.
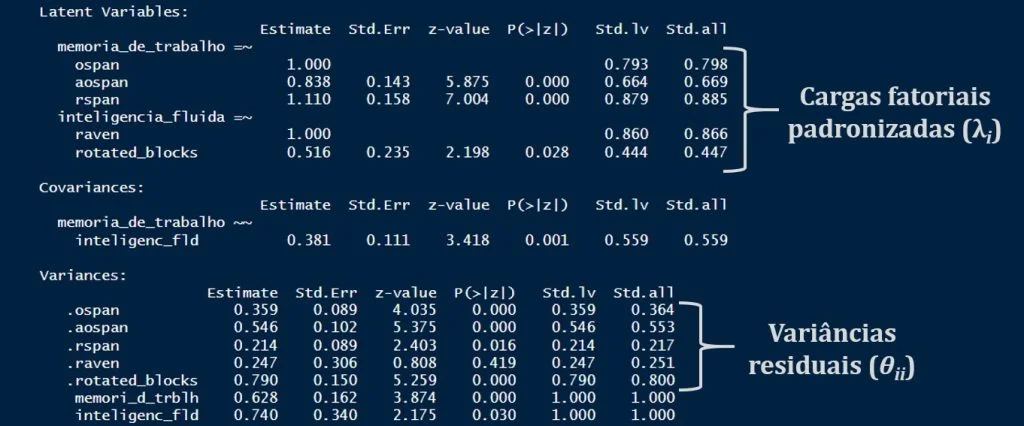
Seria possível escrever uma função para calcular automaticamente a variância média extraída diretamente no R. No entanto, isso foge do escopo deste post. Ao invés disso, mostraremos quais valores da saída anterior usamos para calcular essa medida de fidedignidade.
As cargas fatoriais padronizadas e as variâncias residuais dos indicadores de capacidade de memória de trabalho, contidas na Figura 1, são reapresentadas na Figura 2.

Com base nesses valores, podemos calcular a variância média extraída:

Já a Figura 3 apresenta as cargas fatoriais padronizadas e as variâncias residuais dos indicadores de inteligência fluida.
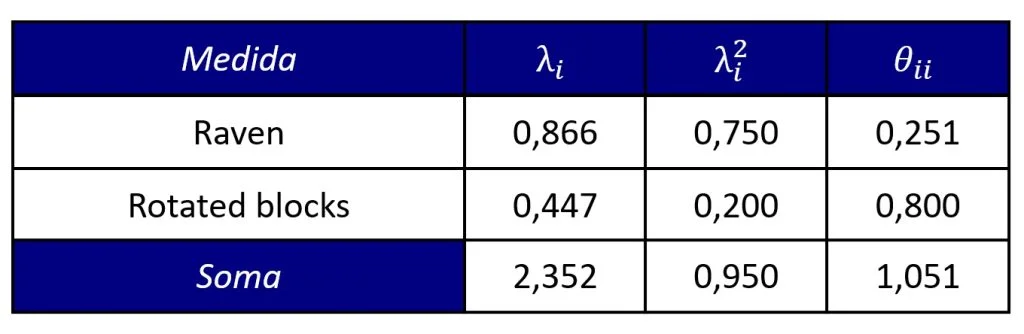
Com base nesses valores, podemos calcular a variância média extraída:
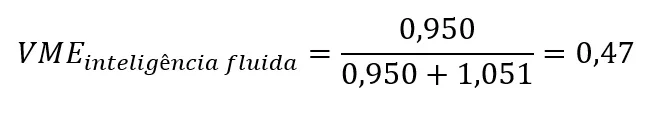
Interpretando os valores de variância média extraída
Em nosso exemplo, obtivemos VME de 0,62 para o fator capacidade de memória de trabalho, enquanto a VME para o fator inteligência fluida foi de 0,47.
Como regra geral, espera-se uma variância média extraída superior a 0,50 como um indicador de ajuste adequado do modelo aos dados. Ou seja, o valor de VME foi satisfatório para o fator capacidade de memória de trabalho, mas não para o fator inteligência fluida.
Um possível ponto de questionamento em nosso exemplo é o baixo número de indicadores por fator. No entanto, salientamos que a escolha de um modelo com poucos indicadores foi feita devido ao caráter didático deste tutorial.
Além disso, vale ressaltar que a variância média extraída não é afetada pelo número de itens (Valentini & Damásio, 2016). Sendo assim, o valor inadequado de VME para o fator inteligência fluida se deve possivelmente à baixa carga fatorial do rotated blocks (λ = 0,447), que puxou para baixo o valor da VME.
Conclusão
Neste post, falamos sobre a variância média extraída. Gostou desse conteúdo? Aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Bandalos, D. L. (2018). Measurement theory and applications for the social sciences. The Guilford Press.
Fornell, C., & Larcker, D. F. (1981). Evaluating structural equations models with unobservable variables and measurement error. Journal of Marketing, 18(1), 39–50. https://doi.org/10.2307/3151312
Unsworth, N., Heitz, R. P., Schrock, J. C., & Engle, R. W. (2005). An automated version of the operation span task. Behavior Research Methods, 37(3), 498–505. https://doi.org/10.3758/BF03192720
Valentini, F., & Damásio, B. F. (2016). Variância média extraída e confiabilidade composta: Indicadores de precisão. Psicologia: Teoria e Pesquisa, 32(2), Article e322225. https://doi.org/10.1590/0102-3772e322225
Como citar este post
Lima, M. (2025, 2 de maio). O que é e como calcular a variância média extraída? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/variancia-media-extraida













