A regressão logística é uma técnica estatística utilizada para prever a probabilidade de ocorrência de um evento, a partir de uma ou mais variáveis preditoras, que podem ser categóricas ou contínuas. Nesse contexto, a variável que queremos prever é chamada de variável de resultado (ou variável dependente), enquanto as variáveis utilizadas para fazer essa previsão são conhecidas como variáveis preditoras (ou variáveis independentes).
Quando a variável de resultado é categórica — por exemplo, se uma pessoa está ou não doente —, a tarefa de prever a categoria correta é chamada de problema de classificação. Embora tais variáveis categóricas possam ser representadas numericamente (e.g., 0 e 1), tais números não possuem propriedades genuinamente quantitativas. Sendo assim, isso exige uma abordagem estatística específica, como a regressão logística.
Quais são os tipos de regressão logística existentes?
Podemos classificar as regressões logísticas tomando como base a(s) variável(eis) preditora(s), a variável de resultado ou ambas.
No que tange à variável de resultado, a regressão logística binária se aplica para casos em que a variável de resultado possui apenas duas categorias, tais como “sim” ou “não”, “vivo” ou “morto”, “doente” ou “não doente”.
Por outro lado, a regressão logística multinomial (ou politômica) se aplica a situações em que a variável de resultado possui mais de duas categorias, como níveis educacionais (fundamental, médio, superior), estilo parental (indulgente, negligente, autoritário, autoritativo) e tipo de resposta em teste de memória (acerto, erro semântico, erro não semântico).
No que tange àquilo que usamos para predizer nossa variável de resultado, podemos usar uma ou múltiplas variáveis preditoras. Análogo ao que acontece na regressão linear, o número de variáveis preditoras determina se chamamos a regressão de simples (apenas uma variável preditora) ou múltipla (duas ou mais variáveis preditoras).
Sendo assim, a Tabela 1 sumariza a nomenclatura das regressões logísticas. Contudo, vale ressaltar que os termos “simples” e “múltipla” podem ser omitidos na descrição dos resultados, ou seja, ficarem apenas implícitos pelo contexto das análises.
| Número de categorias na variável de resultado | Número de variáveis preditoras | Nome do modelo de regressão |
| Duas | Uma | Regressão logística binária simples |
| Duas | Duas ou mais | Regressão logística binária múltipla |
| Três ou mais | Uma | Regressão logística multinomial simples |
| Três ou mais | Duas ou mais | Regressão logística multinomial múltipla |

Como é a representação matemática do modelo de regressão logística?
Revisitando a regressão linear
Anteriormente, afirmamos que, pela falta de propriedades quantitativas dos números designados às categorias de nossa variável de resultado, precisaríamos adaptar nosso modelo estatístico.
Isso acontece porque, na regressão linear, a parametrização do modelo consiste na equação da reta:
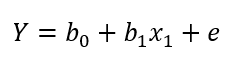
Onde b0 é nosso intercepto, b1 é o coeficiente associado à variável preditora, x1 é a variável preditora, e e é o resíduo do modelo. O modelo anterior se refere à regressão linear simples, mas ele pode ser facilmente generalizado para sua contraparte múltipla, com n variáveis preditoras:
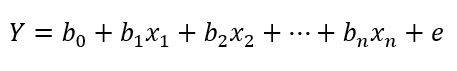
Por exemplo, suponha que queremos predizer os níveis de colesterol LDL (Y) de um conjunto de pacientes, com base em suas respectivas idades (x1). Nesse caso, poderíamos usar uma regressão linear simples. Se quiséssemos incluir preditores adicionais no modelo — por exemplo, sexo biológico (x2) —, teríamos uma regressão linear múltipla.
Note que, no caso anterior, não teremos grandes problemas, pois a variável níveis de colesterol LDL assume valores do conjunto dos números reais. Em outras palavras, níveis de colesterol LDL não é uma variável categórica, que é restrita a poucos valores qualitativos.
Em contrapartida, anomalias acontecerão se tentarmos usar um modelo de regressão linear para predizer uma variável categórica. Por exemplo, suponha que queremos prever se uma mamografia terá resultado negativo (0) ou positivo (1) para câncer de mama, com base na idade da paciente.
A Figura 1 ilustra os resultados de uma regressão linear simples com base nesse exemplo. Note que a linha de regressão não parece ser um modelo adequado para predizer um de dois valores, tal como necessitaríamos que ocorresse quando nossa variável de resultado é binária.
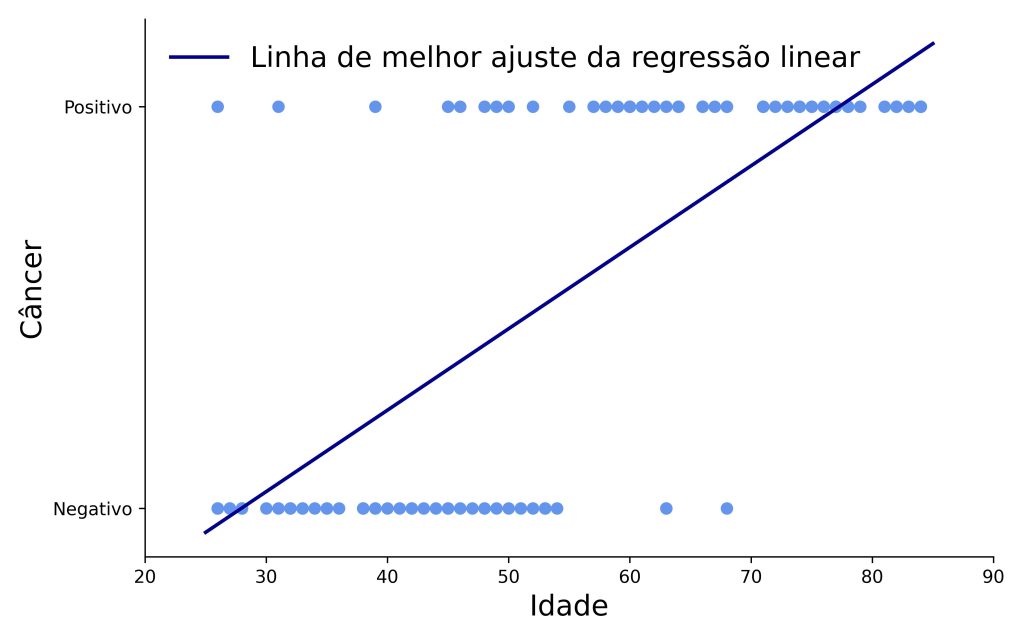
Em seguida, veremos como solucionar este problema.
Introdução à regressão logística binária
Para solucionar o problema descrito na seção anterior, nós adaptamos o modelo de regressão linear para predizermos a probabilidade de ocorrência do evento Y = 1 (em nosso exemplo, 1 = resultado positivo na mamografia). A regressão logística binária (simples) pode ser expressa por:
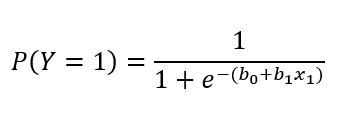
Onde b0 é nosso intercepto, b1 é o coeficiente associado à variável preditora, e x1 é a variável preditora (em nosso exemplo, idade das pacientes). Graficamente, a equação anterior permite o seguinte tipo de modelagem, tal como representado na Figura 2.
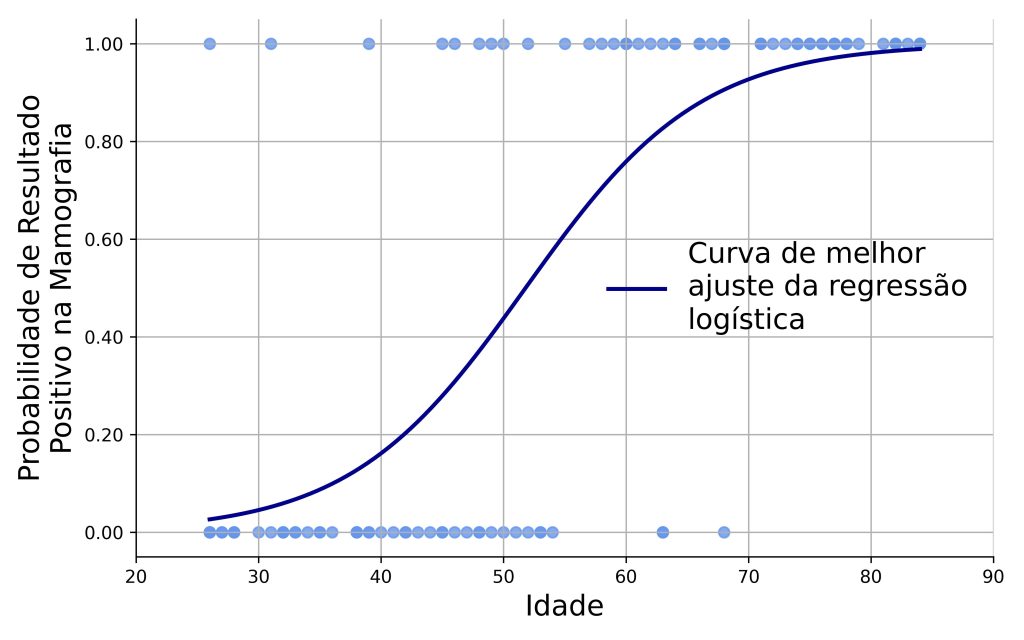
Na prática, a equação anterior pode ser reparametrizada como uma equação da reta, onde a variável de resultado agora é plotada em um espaço logit. Isso é feito de modo a mapearmos valores de probabilidade, que estão restritos ao intervalo [0, 1], ao espaço dos números reais, ]–∞, +∞[.
Nessa reparametrização, o logit da probabilidade P é dado pelo logaritmo natural da chance, cujo resultado pode assumir qualquer valor no conjunto dos números reais. Formalmente:
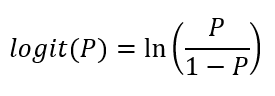
Consequentemente, a Figura 2 pode ser reexpressa na Figura 3, onde a equação da regressão logística é descrita como predizendo o logit da probabilidade de resultado positivo na mamografia:
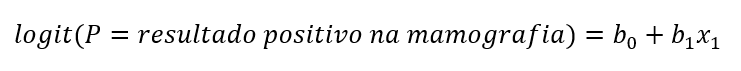
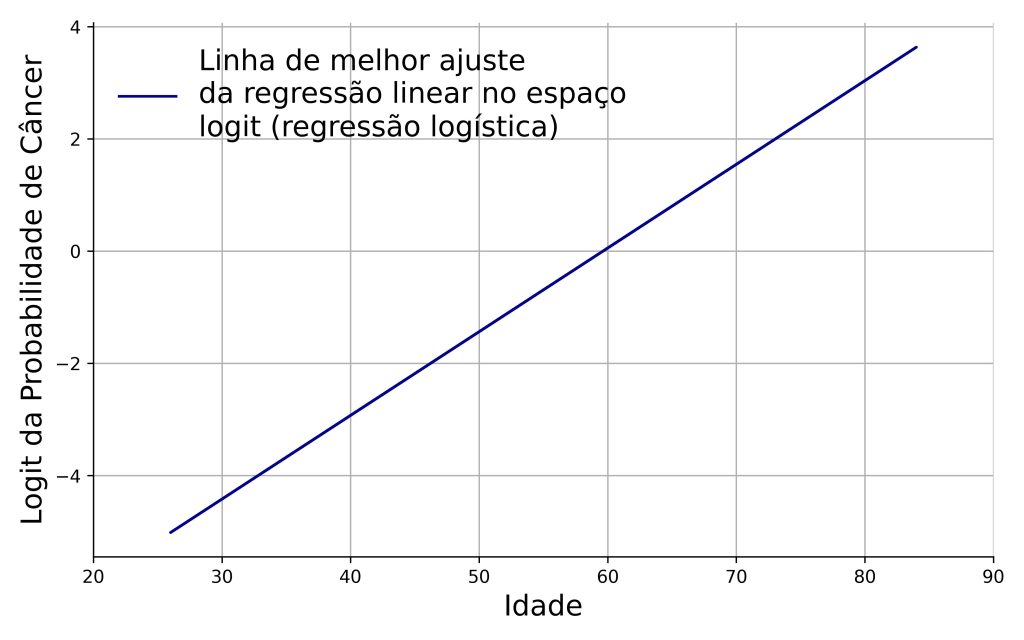
Note que a variável no eixo y agora está em um espaço logit. É essa transformação que permite reparametrizar a curva logística em uma equação da reta, o que torna a modelagem matemática mais simples.
Para concluir a seção, nosso exemplo se restringiu à regressão binária simples, mas a lógica se estende diretamente para sua contraparte múltipla, onde há mais de uma variável preditora. A equação a seguir ilustra a regressão logística binária múltipla:
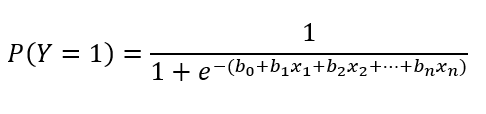
Qual é a diferença entre uma regressão linear e uma regressão logística?
Anteriormente, apresentamos a equação da regressão logística. Aqueles já familiarizados com a regressão linear podem ter notado que sua fórmula está presente no expoente do denominador da equação da regressão logística. Isso ocorre porque a regressão logística é uma espécie de regressão linear com ajuste na função de ligação entre variáveis preditoras e a variável de resultado.
Essa transformação é necessária porque a regressão linear pressupõe que há uma relação linear entre a variável de resultado e as variáveis preditoras. No entanto, isso não acontece como uma variável categórica, cujos valores não fazem parte do conjunto dos números reais.
Desse modo, a adaptação da regressão logística é necessária para levar em conta a relação não linear entre preditores e variável de resultado. Sendo assim, o uso de equações distintas é o que leva em conta as diferentes formas de relacionamento entre variáveis preditoras e variável de resultado.
Consequentemente, a interpretação dos coeficientes é distinta em cada modelo estatístico. Na regressão linear, predizemos um valor real (e.g., nível de colesterol LDL). Em contrapartida, na regressão logística, predizemos a probabilidade de ocorrência de um evento (ou de pertencimento a uma das categorias da variável de resultado categórica).
Você também pode se interessar por: Diferença entre as regressões logísticas: binária, ordinal e multinomial

Quando usar a regressão logística?
Você deve usar a regressão logística sempre que sua variável de resultado for categórica. Ela é especialmente útil quando:
- Há apenas dois possíveis resultados, como “fuma” ou “não fuma”.
- Existem múltiplos resultados, mas você pretende colapsá-los em duas categorias mutuamente excludentes. Por exemplo, você deseja predizer a presença de transtorno da personalidade (borderline, histriônica, narcisista) versus sua ausência, mas sem fazer distinções quanto ao tipo de transtorno da personalidade.
- A variável de resposta possui três ou mais categorias sem ordem específica, como estilos de apego (seguro, evitativo, ambivalente e desorganizado).
- A variável de resposta é ordinal, ou seja, apresenta categorias com ordem, como avaliações de 1 a 5.
Enquanto os dois primeiros exemplos requerem o uso de regressão logística binária, os dois últimos exigem aplicar a regressão logística multinomial.
Como analisar o modelo de regressão logística?
Ao analisar os resultados da regressão logística, podemos avaliar o quão bem o modelo logístico se adequa aos dados através do valor do pseudo R2, que indica a relação entre a variável de resultado e cada um dos preditores, com valores que variam de –1 a 1.
Os valores próximos de zero indicam que não há relação entre preditora e resultado. Valores positivos indicam que o aumento dos valores das variáveis preditoras está associado a um aumento da probabilidade da variável de resultado. Valores negativos indicam que o aumento dos valores das variáveis preditoras está associado a uma diminuição da probabilidade da variável de resultado. Além disso, quanto mais próximo de –1 ou 1, maior é a força da relação.
Também existem outros critérios de avaliação do modelo, como o log-likelihood (LL), o desvio (–2LL) e os critérios de informação de Akaike (AIC) e bayesiano (BIC). Também existem diferentes formas de calcular o pseudo R2, como aquelas propostas por McFadden ou por Cox e Snell, cada qual com suas vantagens e desvantagens.
Saiba mais: Regressão logística: pseudo R2

Exemplo de regressão logística
Uma vez ajustado o modelo de regressão logística, é fundamental avaliá-lo sob diferentes perspectivas. Primeiramente, pode-se analisar a qualidade geral do ajuste por meio de índices como:
- Pseudo R² (como McFadden ou Cox-Snell): mede o grau de associação entre as variáveis preditoras e a variável de resultado. Valores próximos de zero indicam relação fraca ou inexistente; valores próximos de –1 e 1 indicam relação forte negativa e forte positiva, respectivamente.
- Log-likelihood e –2LL: fornecem informações sobre a verossimilhança do modelo. Quanto menor é o seu valor, mais os valores previstos pelo modelo se aproximam dos valores empíricos presentes no banco de dados.
- Critérios AIC e BIC: ajudam a comparar diferentes modelos, penalizando pela complexidade, isto é, o aumento no número de parâmetros em modelos mais complexos.
Além disso, é possível avaliar cada variável preditora individualmente (em nosso exemplo, avaliaremos apenas um preditor, pois se trata de uma regressão simples). O valor de p indica se há uma relação estatisticamente significativa entre a preditora e a variável de resultado. Um possível relato é descrito a seguir:
Conduzimos uma regressão logística binária simples a fim de avaliar se a idade prediz a presença de câncer (0 = sem câncer, 1 = câncer). O modelo foi estatisticamente significativo, χ2(1) = 66,87, p < 0,001, indicando que o modelo contendo a idade contribui em predizer a presença de câncer. O modelo apresentou um pseudo R² de McFadden igual a 0,48, indicando um bom ajuste. Além disso, ele classificou corretamente aproximadamente 85% dos casos com base em um ponto de corte de 0,5.
O coeficiente da regressão logística para a idade foi b = 0,14, EP(b) = 0,03, z = 5,43, p < 0,001. Transformando esse coeficiente em razão de chances, concluímos que, para cada aumento de um ano de idade das pacientes, a chance de diagnóstico de câncer aumenta em 15%, RC = 1,15, IC 95% [1,09, 1,21]. Esses resultados sugerem que a idade é um fator significativo na predição da presença de câncer.
Entendendo a razão de chances (odds ratio)
A razão de chances — também chamada de odds ratio — representa a razão entre a chance de um evento ocorrer e a chance de ele não ocorrer. Em outras palavras, é uma medida que expressa o quanto a presença de uma variável preditora aumenta (ou diminui) a chance de determinado resultado.
Na saída de uma regressão logística, nosso coeficiente está em logit (ou log odds), o que é de difícil interpretação. para retornarmos seu valor à métrica original, calculamos o antilog, isto é, exponenciamos o valor do b:
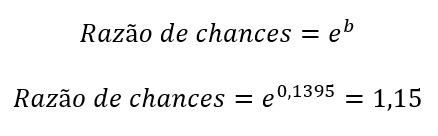
(Podemos fazer o mesmo para os limites de confiança do intervalo de confiança do b, caso seja nossa intenção reportá-los em termos de intervalos de confiança da razão de chances. Assumimos que intervalos de confiança que não incluem o 1 indicam preditores estatisticamente significativos.)
Em nosso exemplo, a idade apresentou uma razão de chances de 1,15, ou seja, para cada aumento de uma unidade na idade, a chance de ter câncer aumenta em 15%. Isso sugere uma relação positiva entre as variáveis.
Quando a razão de chances é menor que 1, interpretar seu valor é um pouco mais difícil. Nesse caso, é interessante inverter a direção da medida. Por exemplo, suponha que o coeficiente relacionado a um preditor seja b = 0,80. Nesse caso, para invertê-lo, basta calcular:
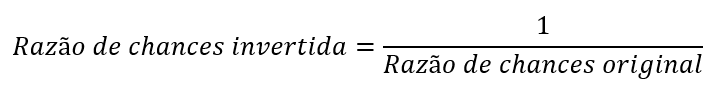
Em nosso exemplo, 1 / 0,80 = 1,25. No entanto, tome cuidado! A interpretação a seguir está incorreta: “as chances de câncer aumentam em 25% para cada aumento de uma unidade na variável preditora”.
Como nós invertemos a razão de chances, nossa interpretação também muda de direção. Eis a interpretação correta: “a cada uma unidade de aumento na variável preditora, as chances de câncer diminuem em 25%”.
Saiba mais: Razão de chances (odds ratio): o que é, como calcular e como interpretar?
Conclusão
Gostou desse conteúdo? Aproveite e também se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Hair, J. F., Jr., Black, W. C., Babin, B. J., Anderson, R. E., & Tatham, R. L. (2009). Análise multivariada de dados (6ª ed.). Artmed.
Como citar este post
Lima, M. (2025, 4 de abril). O que é regressão logística? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-regressao-logistica/














