O que é multicolinearidade?
A multicolinearidade ocorre quando duas ou mais variáveis independentes de um modelo de regressão linear múltipla apresentam alta correlação entre si. Embora pareça apenas um detalhe técnico, esse fenômeno pode distorcer as estimativas dos coeficientes, prejudicar a interpretação dos resultados e comprometer a validade da análise.
Para entender o impacto, imagine que você deseja estimar os efeitos da renda, da escolaridade e do estado civil sobre a satisfação com a vida. No entanto, no Brasil, renda e escolaridade tendem a estar altamente correlacionadas — isto é, quem tem maior escolaridade tende a ter maior renda, e vice-versa.
Isso significa que o modelo pode ter dificuldade em distinguir a contribuição única de cada uma dessas variáveis em predizer a variável dependente.
Portanto, identificar e lidar com a multicolinearidade é essencial antes de interpretar os resultados de um modelo. Em seguida, explicamos como diagnosticar esse problema e quais são as estratégias mais eficazes para resolvê-lo.

Como identificar a multicolinearidade?
Saber o que é multicolinearidade ajuda o pesquisador a detectar seus sinais com mais precisão. Uma das formas mais simples de identificação é observar a matriz de correlação entre variáveis preditoras. Quando os coeficientes de correlação ultrapassam 0,70 ou, pior ainda, 0,80, há um alerta importante.
No entanto, a matriz de correlação captura apenas relações bivariadas. Por isso, usamos também o fator de inflação da variância (variance inflation factor, VIF), que mede quanto a variância de um coeficiente está inflada devido à correlação com outros preditores. VIFs entre 5 e 10 já indicam atenção; valores acima de 10 indicam um problema sério.
Vale destacar que o termo multicolinearidade se aplica a situações com três ou mais variáveis que apresentam relações altamente lineares entre si — com apenas duas variáveis, é conceitualmente mais preciso se falar em colinearidade. Assim, quanto maior o número de preditores correlacionados, mais crítico o problema se torna.
Saiba mais: Diagnóstico de multicolinearidade

Como lidar com a multicolinearidade? Três estratégias úteis
Uma vez que você entenda o que é multicolinearidade e consiga identificá-la, o próximo passo é decidir como enfrentá-la. Em seguida, listamos três abordagens práticas.
Exclusão de variáveis redundantes
A abordagem mais direta é remover uma das variáveis correlacionadas. Como há redundância, a exclusão pode não prejudicar a análise. No entanto, é fundamental considerar o papel teórico da variável excluída, pois sua retirada pode comprometer a interpretação.
Por exemplo, suponha que um pesquisador esteja analisando fatores que influenciam o risco cardiovascular e inclua, entre os preditores, tanto o colesterol total quanto o LDL (lipoproteína de baixa densidade).
Como o LDL compõe grande parte do colesterol total, essas variáveis tendem a estar altamente correlacionadas. Sendo assim, excluir o colesterol total e manter apenas o LDL — que é considerado clinicamente mais específico para o risco cardiovascular — pode ser uma decisão estatística e teoricamente justificada.
Redução de dimensionalidade
Outra alternativa é agrupar as variáveis correlacionadas por meio de técnicas como a análise de componentes principais. Em vez de várias variáveis altamente correlacionadas, você passa a usar um único escore composto. Isso torna o modelo mais parcimonioso, embora se perca a interpretação individual de cada preditor.
Imagine que você está interessado em prever o índice de produtividade de profissionais a partir de variáveis como número de horas trabalhadas por semana, número de projetos em andamento, frequência de reuniões e tempo médio de dedicação por projeto. Essas variáveis mensuram diferentes aspectos do volume de trabalho e tendem a estar altamente correlacionadas entre si.
Como elas representam dimensões complementares de um mesmo construto (carga de trabalho), faz sentido aplicar uma análise de componentes principais. O resultado seria um único escore que resume essa carga, eliminando a multicolinearidade e mantendo a essência formativa do modelo — ainda que a contribuição individual de cada variável se torne menos evidente.
Modelagem por equações estruturais
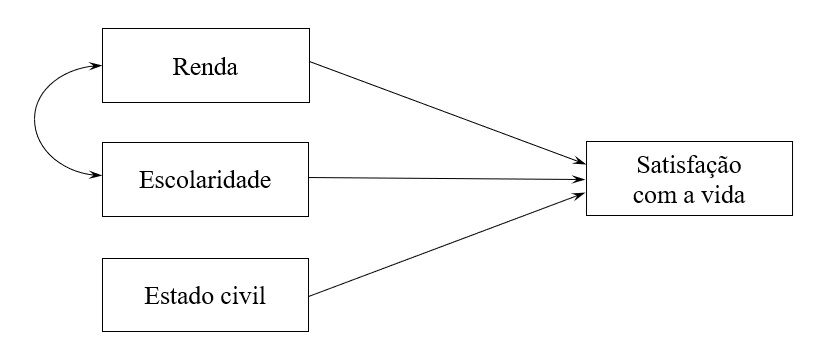
Por fim, se o objetivo for manter todas as variáveis no modelo, mesmo que correlacionadas, uma saída sofisticada é a modelagem por equações estruturais. Essa abordagem permite estimar diretamente a correlação entre preditores (como uma seta bidirecional entre renda e escolaridade; Figura 2) e isolar seus efeitos sobre a variável dependente. Assim, o modelo é “purificado”, sem distorções causadas pela multicolinearidade.
Conclusão
Gostou deste conteúdo? Então aproveite e também se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Como citar este post
Damásio, B. (2021, 3 de maio). O que é multicolinearidade, como identificar e como lidar? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-multicolinearidade/