Quando conduzimos múltiplos testes estatísticos, a probabilidade de cometermos pelo menos um erro Tipo I aumenta. A fim de controlar essa taxa de erros no conjunto de testes, precisamos realizar algum tipo de ajuste. Um dos ajustes mais conhecidos é a correção de Bonferroni, que será o tema do post de hoje.
Teste de hipótese, erro Tipo I, erro Tipo II e nível de significância
Antes de mais nada, vamos definir alguns conceitos. Quando realizamos um teste de significância da hipótese nula (ou teste de hipótese, para fins de brevidade), temos duas hipóteses relevantes.
A hipótese nula (H0) é aquela que tentamos falsear com nossos dados. Comumente, essa hipótese afirma que um efeito ou associação entre variáveis não existe. Já a hipótese alternativa (H1) afirma o oposto, ou seja, que existe um efeito ou relação entre variáveis.
No entanto, os resultados de nossas pesquisas são probabilísticos, o que implica que podemos cometer erros. O erro Tipo I consiste em rejeitar uma hipótese nula verdadeira. Por exemplo, se concluirmos que um medicamento reduz a enxaqueca, quando ele na verdade não reduz, teremos cometido um erro Tipo I.
Em contrapartida, o erro Tipo II consiste em falhar em rejeitar uma hipótese nula falsa. Por exemplo, se concluirmos que um medicamento não reduz a enxaqueca, quando ele de fato a reduz, teremos cometido um erro Tipo II (Figura 1).
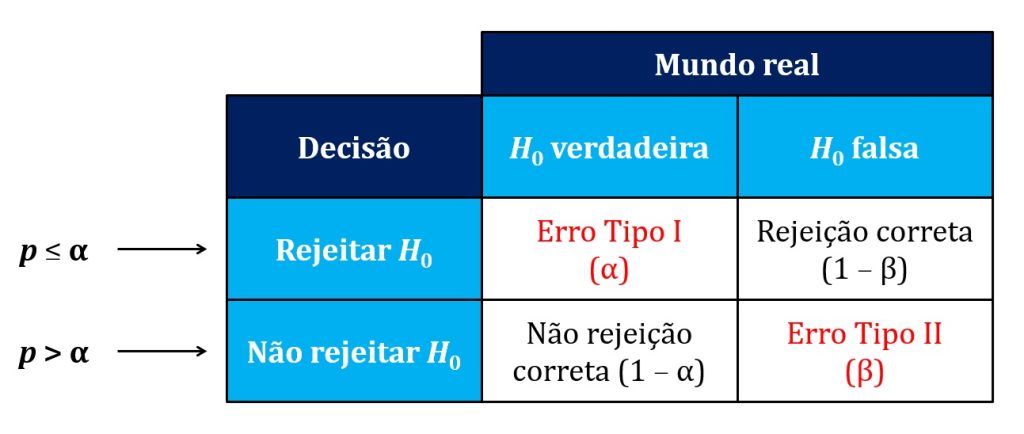
No contexto do teste de hipótese, o nível de significância representa a probabilidade de rejeitarmos a hipótese nula, se ela for verdadeira. Esse valor deve ser definido pelo pesquisador antes das análises. Para avaliarmos se nossos resultados são ou não estatisticamente significativos, comparamos nosso valor de p obtido nas análises com o nível de significância previamente definido.

O que é familywise e experimentwise error rates?
Estudos científicos comumente envolvem múltiplas hipóteses. Considere, por exemplo, que investigamos a efetividade de três métodos de ensino do português (A, B, C) em crianças com línguas nativas distintas (espanhol, inglês, japonês, sueco). Implementamos o tratamento por seis meses, medindo a compreensão e a produção da linguagem pré- e pós-tratamento.
Nesse delineamento, analisamos os escores de compreensão por meio de uma análise de variância (ANOVA) fatorial mista 2 (pré-tratamento, pós-tratamento) × 3 (método, A, método B, método C) × 4 (espanhol, inglês, japonês, sueco).
Essa ANOVA produzirá três efeitos principais (tempo, método de ensino, língua nativa), três efeitos de interação (Tempo × Método de Ensino, Tempo × Língua Nativa, Método de Ensino × Língua Nativa) e um efeito de interação de segunda ordem (Tempo × Método de Ensino × Língua Nativa).
Nesse contexto, o familywise error rate diz respeito à probabilidade de pelo menos um erro Tipo I em uma série ou “família” de testes relacionados. Quando conduzimos vários testes, como em nossa ANOVA, nós aumentamos a probabilidade de encontrar efeitos espúrios simplesmente por termos conduzido muitos testes.
No exemplo anterior, a ANOVA com sete efeitos produziria um familywise error rate de 30,2%. O problema se agravaria ainda mais pelo fato de termos que conduzir testes post hoc, por exemplo, em caso de efeito significativo da língua nativa, de modo a identificarmos quais grupos diferiram entre si.
Ademais, como temos duas variáveis dependentes em nosso estudo, conduziremos uma segunda ANOVA, mas agora considerando a medida de produção em nosso testes. Além disso, eventualmente podemos conduzir análises correlacionais entre os escores nas duas medidas.
Nesse caso, também inflacionaremos o experimentwise error rate, que se refere à probabilidade de pelo menos um erro Tipo I em uma série de análises de um mesmo experimento.
O que é e para que serve a correção de Bonferroni?
A correção de Bonferroni é um método para corrigir os níveis de significância de nossos testes de hipóteses quando conduzimos vários testes consecutivos. Seu principal uso costuma ser nos testes post hoc da ANOVA, quando conduzimos vários testes t para identificar quais grupos diferem entre si.
Em nosso exemplo dos métodos de ensino do português para crianças com outra língua nativa, um efeito global da língua nativa seria possivelmente explorado por meio de seis comparações em pares, conforme ilustramos na Figura 2.

O problema é que quando conduzimos vários testes em sequência, há uma maior probabilidade de pelo menos um dos valores de p serem menores que nosso nível de significância. Podemos detectar, por exemplo, que falantes do inglês se saem melhor na produção da linguagem que falantes do japonês, mesmo que essa diferença seja apenas devido a variação amostral.
Como calcular a correção de Bonferroni?
Com a correção de Bonferroni, vamos ter um novo valor de significância (o valor alfa, α) que leva em consideração a quantidade de testes realizados. Ou seja, compararemos o nosso valor de p com um αajustado, e não mais com o αoriginal. Com isso, precisaremos de evidências mais surpreendentes para rejeitarmos a hipótese nula. Calcular o valor ajustado é simples:
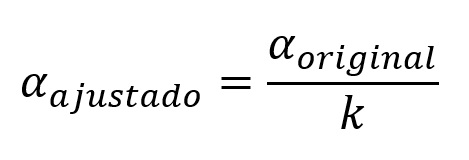
onde k corresponde ao número de comparações.
Vamos supor, por um momento, que o conjunto de testes que queremos considerar na aplicação da correção de Bonferroni se restringe ao fator língua nativa, da ANOVA. Desse modo, nosso teste post hoc envolverá seis comparações. Assumindo-se αoriginal = 0,05, teremos, portanto:
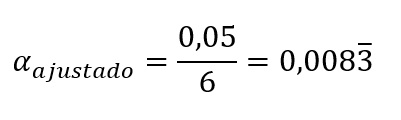
Ou seja, com esta correção, nós apenas rejeitaremos a hipótese nula quando um valor de p das comparações post hoc for menor que 0,0083.
Uma maneira de pensar na correção de Bonferroni é por meio de uma metáfora. Por exemplo, em uma prova de salto em altura, uma atletista precisa saltar sobre uma barra localizada a uma determinada distância do chão, sem derrubá-la (Figura 3). Podemos pensar na altura da barra como nosso nível de significância original.

No entanto, como ela terá a oportunidade de realizar múltiplos saltos, elevaremos um pouco a altura da barra, de modo a corrigir nosso critério para tentativas múltiplas. Essa elevação da barra corresponde à diminuição de nosso alfa ajustado por meio da correção de Bonferroni.
Correção de Bonferroni e o equilíbrio entre erros dos Tipos I e II
A correção de Bonferroni tende a inflar a probabilidade de erro do Tipo II, principalmente quando estamos lidando com um número muito grande de testes.
Por exemplo, a correção de nosso α para 10 comparações de interesse é dada por α = 0,05/10 = 0,005. Agora, suponha que quatro de nossas 10 comparações tenham ps entre 0,01 e 0,04. Contudo, a correção de Bonferroni nos levaria a falhar em identificar efeitos em nossa amostra, pois ela tornou nosso nível de significância muito exigente.
Por isso, é preciso pesar se, em sua pesquisa, é mais importante diminuir o erro Tipo I ou o erro Tipo II. Armstrong (2014) oferece sugestões de quais pontos devemos considerar a fim de tomarmos nossa decisão.
Nenhuma correção deve ser feita nestas circunstâncias:
- O estudo é restrito a um número pequeno de comparações planejadas;
- O estudo é exploratório, com testes post hoc que servirão somente para gerar hipóteses para estudos subsequentes;
- O estudo inclui múltiplos testes t ou múltiplas correlações, mas é o resultado individual dos testes que importa;
- É essencial evitar o erro Tipo II (e.g., detecção de problemas em protocolos de segurança em aviação).
Em contrapartida, devemos considerar a correção de Bonferroni quando:
- O estudo contém uma “hipótese nula universal”, de forma que o importante é que todos os testes devem ser não significativos para que se rejeite a hipótese nula;
- É essencial evitar o erro Tipo I (e.g., aprovação errônea de novo medicamento ou tratamento);
- Um número grande de testes foi realizado, mas sem o planejamento prévio para determinar quais resultados são significativos.
Conclusão
Neste post, você aprendeu o que é e como calcular a correção de Bonferroni. Esperamos que este post tenha ajudado você a entender melhor esses conceitos e como aplicá-los na prática. Aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Armstrong, R. A. (2014). When to use the Bonferroni correction. Ophthalmic and Physiological Optics, 34(5), 502–508. https://doi.org/10.1111/opo.12131
Howell, D. C. (2013). Multiple comparisons among treatment means. In D. C. Howell, Statistical methods for psychology (8th ed., pp. 369–410). Wadsworth Cengage Learning.
Como citar este post
Lima, M. (2025, 22 de janeiro). O que é correção de Bonferroni? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/correcao-bonferroni/















Uma resposta