Na pesquisa quantitativa, é comum que pesquisadores desejem testar múltiplas hipóteses. Por exemplo, em um estudo envolvendo cinco medidas contínuas, poderíamos avaliar 10 correlações entre pares de variáveis. Em tais situações, um conceito relevante que você precisa conhecer é o familywise error rate.
Neste post, entenderemos o significado e a importância desse conceito. Além disso, mostraremos como estimar essa taxa de erros. Por fim, apresentaremos algumas técnicas propostas para controlar essa taxa de erros em seus estudos.
O que é familywise error rate (FWER)?
No teste de significância da hipótese nula, a hipótese nula (H0) é aquela que buscamos nulificar, isto é, refutar. Tradicionalmente, essa hipótese afirma que não existe efeito ou relação entre variáveis. Já a hipótese alternativa (H1) afirma o contrário, ou seja, que existe um efeito ou relação entre variáveis.
Para testarmos nossas hipóteses, nós primeiramente definimos o nível de significância (α, letra grega alfa) que adotaremos, que representa a probabilidade de rejeitarmos a hipótese nula, se ela for verdadeira. Por exemplo, se adotarmos α = 0,05, então esperamos que a frequência a longo prazo de cometermos um erro Tipo I seja de 5%.
No entanto, considere agora um estudo individual, que realiza vários testes estatísticos. Por exemplo, nos testes post hoc de uma ANOVA envolvendo três grupos, nós realizamos três comparações: Grupo 1 vs. Grupo 2, Grupo 1 vs. Grupo 3 e Grupo 2 vs. Grupo 3.
O problema das comparações múltiplas é que elas aumentam a probabilidade de achados espúrios, isto é, que não refletem fenômenos reais. Sendo assim, podemos definir familywise error rate como a probabilidade de cometer pelo menos um erro Tipo I em uma família de testes.
O termo familywise error rate pode ser abreviado por FWER, e traduzido por taxa de erros da família dos testes ou taxa de erro familiar, onde família se refere a um conjunto de análises relacionadas. Eventualmente, metodólogos também se referem ao conceito como experimentwise error rate (taxa de erros de um experimento), mas aqui adotaremos o primeiro termo em inglês, para fins de consistência.

Qual é a diferença entre nível de significância e familywise error rate?
A diferença entre nível de significância e familywise error rate é sutil, mas importante. O nível de significância diz respeito à probabilidade (ou frequência relativa no longo prazo) de erro Tipo I. Por exemplo, ao conduzirmos 100 testes independentes, adotando α = 0,05, esperamos que cinco deles sejam estatisticamente significativos, caso a hipótese nula seja verdadeira.
Em contrapartida, o familywise error rate diz respeito à probabilidade de pelo menos um erro Tipo I em uma série de testes. Sendo assim, à medida que realizamos mais testes, o familywise error rate aumenta conforme a seguinte fórmula:
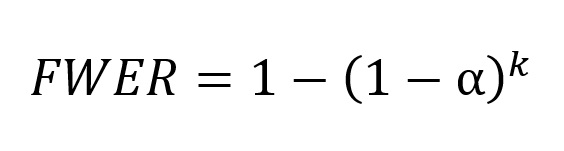
onde k é o número de testes. No exemplo das comparações post hoc da ANOVA que mencionamos anteriormente, teríamos:
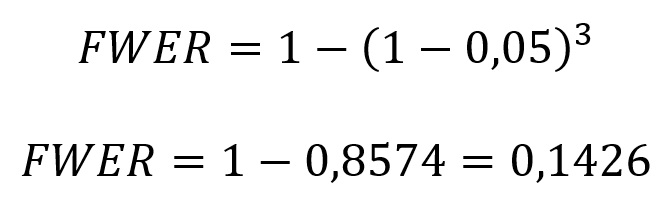
Em outras palavras, quando fazemos três comparações em pares, estimamos uma probabilidade de 14,26% de pelo menos um erro Tipo I.
Vale ressaltar, contudo, que a fórmula anterior se aplica a cenários em que as comparações são independentes. Na prática, as comparações post hoc de uma ANOVA não são independentes, pois o mesmo grupo contribui para mais de uma comparação par a par.
De maneira similar, quando temos testes t para grupos independentes comparando os mesmos grupos em diferentes medidas (e.g., frequência cardíaca, pressão sistólica, pressão diastólica, IMC), nossas comparações não são genuinamente independentes. Contudo, podemos considerar que a fórmula anterior é uma boa aproximação para o limite superior do familywise error rate mesmo em comparações dependentes.
Familywise error rate em função do número de comparações e do nível de significância
Com base na fórmula que introduzimos, podemos analisar o impacto do número de comparações e do nível de significância sobre a probabilidade de pelo menos um erro Tipo I. Mostramos esse impacto na Figura 1.
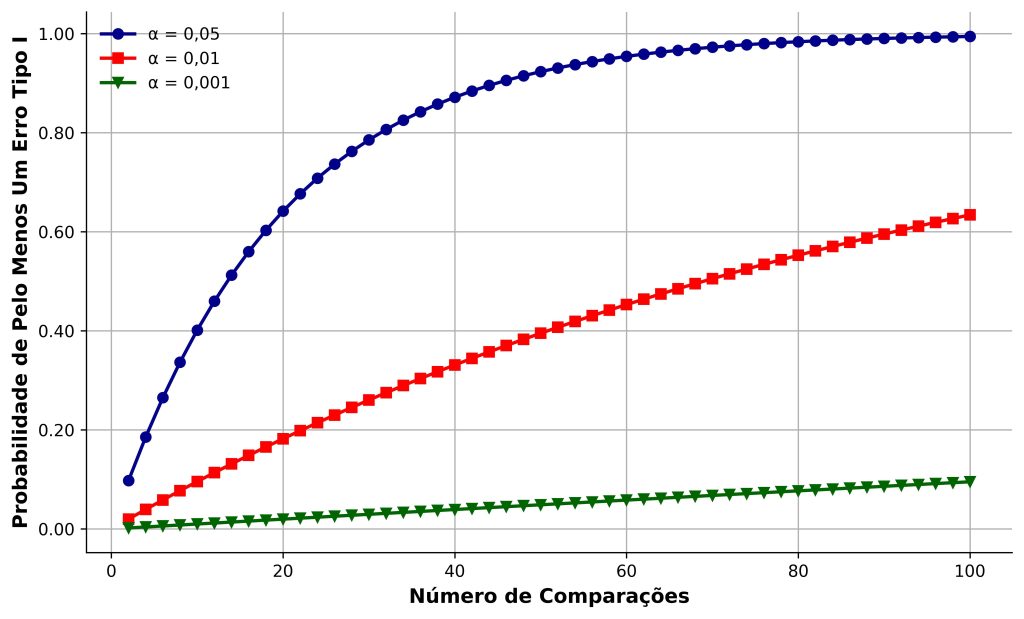
Na Figura 1, consideramos o tradicionalmente usado α = 0,05, bem como duas alternativas mais conservadoras (α = 0,01 e α = 0,001). Primeiramente, quando α = 0,05, mesmo 10 comparações em pares já inflacionam o familywise error rate para 40%. Ou seja, se realizarmos correlações bivariadas entre cinco variáveis (10 correlações), temos 4 chances em 10 de identificarmos pelo menos uma correlação significativa se todas as hipóteses nulas forem verdadeiras.
Mesmo quando adotamos níveis de significância mais conservadores (α = 0,01 e α = 0,001), o familywise error rate cresce monotonicamente em função do aumento do número de comparações. Por exemplo, com 40 comparações, o familywise error rate será de 33% e de 3,9% para α = 0,01 e α = 0,001, respectivamente, indicando que podemos rejeitar hipóteses nulas verdadeiras simplesmente por termos conduzido muitos testes.
Qual a importância de controlar o familywise error rate?
Controlar o familywise error rate é essencial para evitar conclusões enganosas. Em situações onde realizamos múltiplos testes esatísticos, as chances de encontrarmos resultados significativos por mero acaso aumenta.
Ademais, o problema se agrava quando pesquisadores não têm hipóteses claras para seus testes. Isso pode levar ao relato seletivo dos resultados estatisticamente significativos (i.e., p-hacking) ou a formulação a posteriori de hipóteses para os os resultados significativos, de tal modo que tais hipóteses pareçam ter sido concebidas a priori (i.e., HARKing).
Sendo assim, se não controlarmos o familywise error rate, podemos basear nossas decisões em “descobertas” que são, na realidade, falsos positivos.
Imagine que um pesquisador investigue a eficácia de diferentes técnicas psicoterapêuticas no tratamento da ansiedade. Os participantes são designados aleatoriamente a um de três tratamentos, a saber, terapia cognitivo-comportamental (TCC), terapia de aceitação e compromisso (ACT) e controle de lista de espera.
Após uma ANOVA, descobre-se que existe uma diferença significativa nos níveis de ansiedade entre os grupos. No entanto, a ANOVA é um teste global. Para determinar exatamente onde estão as diferenças, o pesquisador realiza testes post hoc entre os grupos (TCC vs. ACT, TCC vs. controle e ACT vs. controle).
Sendo assim, se cada teste post hoc for realizado com um α = 0,05, a probabilidade de detectar pelo menos uma diferença aumenta com o número de comparações. Como vimos anteriormente, com um α = 0,05 e três comparações, o familywise error rate será de 14,26%.
Como controlar o familywise error rate?
Metodólogos propuseram diferentes técnicas de controle do familywise error rate. Em seguida, descrevemos as principais delas.
Correção de Bonferroni
A correção de Bonferroni é uma das técnicas mais simples de compreender, pois ela envolve simplesmente ajustar o nível de significância dividindo-o pelo número de testes realizados (k):
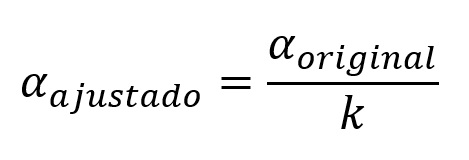
Por exemplo, no caso do experimento envolvendo técnicas psicoterapêuticas, o pesquisador poderia corrigir o α = 0,05/3 = 0,0167. Sendo assim, a afirmação de significância estatística nos testes post hoc agora seriam condicionadas a valores de p menores que 0,0167 (ao invés de menores que 0,05).
Embora essa técnica seja fácil de aplicar, ela pode ser demasiadamente conservadora, sobretudo quando o número de comparações aumenta. Isso pode aumentar a probabilidade de erro Tipo II, isto é, de falharmos em rejeitar uma hipótese nula falsa.
Por exemplo, suponha que temos 10 comparações de interesse; portanto, α = 0,05/10 = 0,005 e FWER = 1 – (1 – 0,005)10 = 0,048889. Agora, suponha que quatro de nossas 10 comparações tenham ps entre 0,01 e 0,04. No entanto, a “supercorreção” da correção de Bonferroni nos levaria a falhar em identificar efeitos genuínos em nossa amostra.
Correção de Tukey
Uma das técnicas post hoc mais populares após uma ANOVA, a correção de Tukey ajusta as probabilidades de comparações múltiplas considerando as correlações entre os testes.
Em síntese, a correção de Tukey considera o valor crítico (q) de uma distribuição de amplitude estudentizada e o multiplica pela estimativa do termo de erro do teste t. Esse valor define a diferença honestamente significativa de Tukey, ou seja, o menor valor necessário de diferença entre comparações para que um resultado seja estatisticamente significativo.
A correção de Tukey é menos conservadora que a correção de Bonferroni, sendo mais adequada para situações em que as comparações são interdependentes.
Correção de Holm-Bonferroni
Esta é uma versão em sequência da correção de Bonferroni. Ao contrário da correção de Bonferroni tradicional, que ajusta o α da mesma forma para todos os testes, o método de Holm-Bonferroni ajusta o α de forma mais flexível.
Por exemplo, suponha que você obteve os seguintes valores de p no experimento envolvendo psicoterapias: TCC vs. ACT (p = 0,54); TCC vs. controle (p = 0,004); ACT vs. controle (p = 0,02). Na correção de Bonferroni, nós primeiramente ordenamos (i.e., ranqueamos) os valores p do menor para o maior (Figura 2).
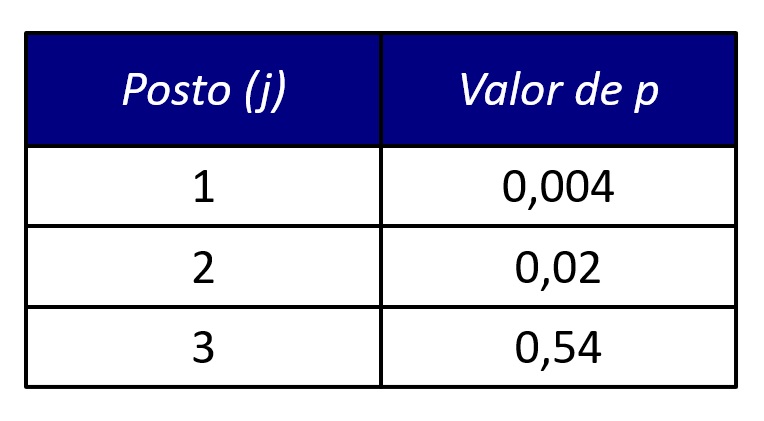
Na correção de Holm-Bonferroni, cada comparação (k) terá um nível de significância distinto, correspondente ao seu posto j na sequência de valores ps, conforme a seguinte fórmula:
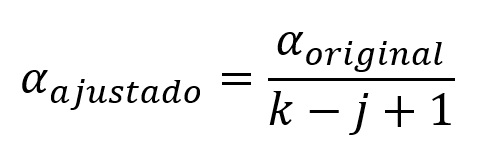
Em nosso exemplo, teríamos os seguintes níveis de significância após a correção de Holm-Bonferroni (Figura 3).
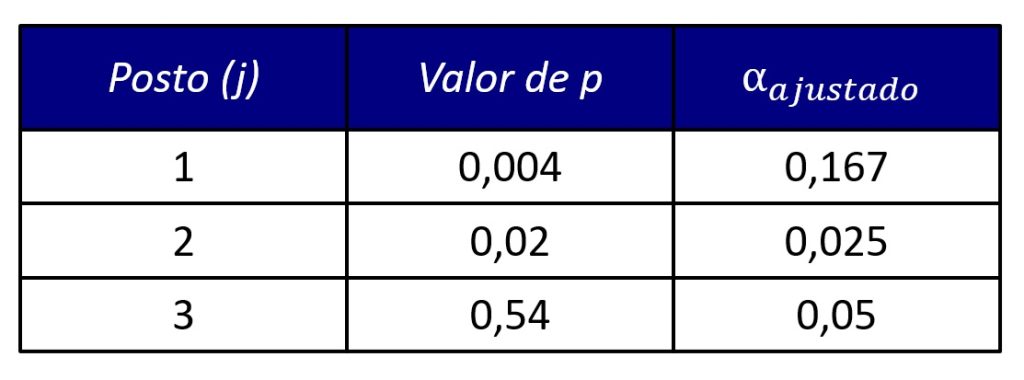
Note que o nível de significância do menor valor de p é semelhante à correção de Bonferroni tradicional, pois o termo j – 1 se anula, tornando a fórmula idêntica àquela da correção de Bonferroni. Em contrapartida, nas demais comparações, a correção de Holm-Bonferroni é menos rigorosa q a correção de Bonferroni tradicional.
Consequentemente, afirmaríamos que há diferenças significativas nas comparações TCC vs. controle e ACT vs. controle sob a correção de Holm-Bonferroni, mas apenas na comparação TCC vs. controle sob a correção de Bonferroni.
Correção de Scheffé
A correção de Scheffé é particularmente útil quando se realizam testes de hipóteses em modelos lineares gerais (como a ANOVA) e quando as comparações não são apenas entre pares de grupos, mas podem envolver comparações mais complexas.
Por exemplo, ao invés de compararmos os grupos em pares, poderíamos comparar TCC e ACT vs. controle. Nesse caso, realizaríamos um contraste entre dois grupos experimentais e um grupo controle. Por se basear na estatística F da ANOVA, a correção de Scheffé é mais flexível para esses propósitos do que outros tipos de correção.
Em contrapartida, a correção de Scheffé é mais conservadora, isto é, possui menor poder estatístico. Em outras palavras, a correção de Scheffé pode aumentar a probabilidade de erro Tipo II.
Correção de Šidák
A correção de Šidák assume que as comparações são independentes entre si. Ela é uma forma ajustada da correção de Bonferroni, com o objetivo de manter o mesmo nível de significância global, mas de maneira mais eficiente em termos de poder estatístico. Sua fórmula é dada por:
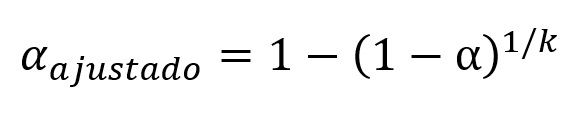
Considerando-se três comparações (k = 3), o valor do α ajustado é de 0,0169, um valor ligeiramente mais liberal do que a correção de Bonferroni.
Atualmente, os softwares estatísticos dispõem dessas correções, que por padrão muitas vezes são aplicadas de maneira automática (Bonferroni ou Tukey) ao realizar as comparações entre grupos, por exemplo, nos post hoc da ANOVA.
Conclusão
Neste post, introduzimos o conceito de familywise error rate, sua importância, bem como algumas maneiras de controlar esse erro. A realização de múltiplos testes estatísticos aumenta as chances de rejeitarmos pelo menos uma das hipóteses nulas verdadeiras em nosso estudo. Por isso, é crucial entender e controlar essa taxa de erro, para garantir que nossas conclusões sejam válidas e confiáveis.
Esperamos que este post tenha ajudado você a entender melhor esses conceitos e como aplicá-los na prática. Aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Armstrong, R. A. (2014). When to use the Bonferroni correction. Ophthalmic & Physiological Optics, 34(5), 502–508. https://doi.org/10.1111/opo.12131
Howell, D. C. (2013). Multiple comparisons among treatment means. In D. C. Howell, Statistical methods for psychology (8th ed., pp. 369–410). Wadsworth Cengage Learning.
Como citar este post
Lima, M. (2025, 21 de janeiro). Familywise error rate (FWER): O que é e como controlar? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/family-wise-error-rate-fwer-o-que-e-e-como-controlar/














