Neste post, falaremos sobre médias marginais. Nosso objetivo é te mostrar a importância das médias marginais na pesquisa científica, bem como te ensinar a diferenciá-las das médias brutas. Este guia abrangente não apenas explica o conceito e a utilidade das médias marginais, mas também destaca suas distinções essenciais.
Exemplo motivador
Considere que coletamos dados sobre 100 adultos fisicamente ativos, referentes ao estado civil de cada participante (solteiro, casado), horário de prática de exercícios (manhã, tarde, noite) e qualidade do sono, que mensuramos por meio de um instrumento de autorrelato.
A Tabela 1 apresenta as médias brutas da qualidade do sono em função do estado civil dos participantes.
| Estado Civil | Média |
| Solteiro (n = 45) | 54,13 |
| Casado (n = 55) | 53,79 |
A Tabela 2, por sua vez, apresenta as médias brutas da qualidade do sono em função do horário de prática de exercícios dos participantes.
| Horário de Prática de Exercícios | Média |
| Manhã (n = 30) | 49,06 |
| Tarde (n = 50) | 59,88 |
| Noite (n = 20) | 54,57 |
Embora as Tabelas 1 e 2 sejam informativas de como o estado civil e o horário de prática de exercícios, respectivamente, impactam na qualidade média do sono, aqui estamos considerando apenas médias brutas. Em outras palavras, estamos considerando o impacto de cada fator isoladamente, sem considerar os níveis do outro fator.
Sendo assim, é importante reconhecermos a necessidade de irmos além, considerando possíveis vieses decorrentes de variações no número de observações por grupo e das covariâncias entre diferentes variáveis.
A pergunta-chave torna-se: como podemos levar essas influências em consideração ao calcular as médias?
Em seguida, veremos a resposta a essa pergunta.

O que são médias brutas?
Anteriormente, apresentamos as médias brutas, que consistem na soma dos escores de um grupo dividido pelo total de escores.
No entanto, essas médias brutas podem ser tendenciosas, uma vez que o número de observações em cada grupo pode ser diferente. Além disso, pode haver alguma covariância oculta ou mediação com outras variáveis no conjunto de dados, criando uma influência “espúria” nas médias.
O que são médias marginais?
De maneira alternativa, podemos analisar as médias modelando seus valores estatisticamente, em vez de simplesmente descrevê-las conforme aparecem nos dados. E isso é feito por meio das médias marginais.
Em síntese, as médias marginais consistem em médias extraídas de um modelo estatístico. Elas representam a média da variável de resposta (em nosso exemplo, a qualidade do sono) para cada nível de cada uma das variáveis preditoras (em nosso exemplo, estado civil e horário de atividade física).
As médias marginais são calculadas com base nos coeficientes estimados em um modelo estatístico como, por exemplo, a análise de variância (ANOVA), e não nas estatísticas calculadas diretamente a partir dos dados brutos. Isso significa que nosso software:
- Estima a média para cada célula do delineamento com base no modelo ajustado (usando os efeitos principais e a interação, caso existam).
- Depois, tira a média dessas previsões ajustadas, assumindo números iguais de participantes por célula.
Em outras palavras, podemos dizer que as médias marginais revelam o valor médio de uma variável, mantendo outras constantes. Diferentemente das médias brutas, elas isolam o impacto de uma variável, sendo cruciais para análises estatísticas como ANOVA, regressão e modelos complexos como estimativas de equações generalizadas.
Por que reportar médias marginais em suas pesquisas?
Reportar médias marginais estimadas oferece diversas vantagens ao pesquisador. Em síntese, elas contribuem para:
- Isolamento de efeitos: elas nos permitem destacar o impacto individual de cada variável, o que é essencial para compreender as contribuições únicas em análises multivariadas.
- Melhor interpretabilidade: ao focar em uma variável por vez, torna-se mais fácil interpretar os resultados, favorecendo a compreensão das contribuições específicas de cada fator.
- Facilidade de comparação: elas facilitam comparações significativas entre os diferentes níveis das variáveis, ajudando a identificar diferenças relevantes em comportamentos ou respostas psicológicas.
Uma metáfora pode ser útil para compreendermos essas vantagens:
Calcular a média bruta de cada grupo é como comparar o desempenho de estudantes sem considerar as disciplinas que eles cursaram. Já as médias ajustadas da ANOVA são como comparar estudantes corrigindo pelas disciplinas diferentes — ou seja, levando em conta que um grupo pode ter feito matérias mais difíceis que o outro.
Exemplo gráfico de médias marginais
Imagine que queremos examinar os efeitos do estado civil e do horário da prática de exercícios sobre a qualidade do sono de 100 adultos que praticam atividades físicas. A fim de avaliar esses efeitos, conduzimos uma ANOVA fatorial 2 × 3. Em seguida, com base nessa ANOVA, calculamos as médias marginais para a qualidade do sono nas diferentes condições do estudo.
Em seguida, plotaremos os dados na Figura 1. Além de apresentarmos as distribuições por meio de boxplots, também apresentamos as médias brutas (círculos) e as médias marginais estimadas (quadrados) para cada célula do delineamento.
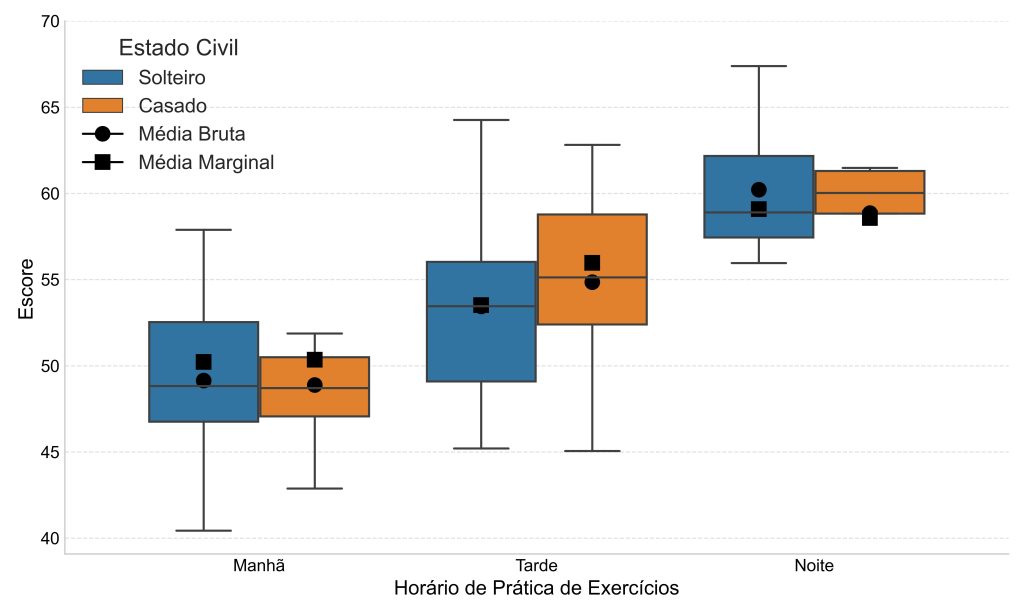
A Figura 1 nos ajuda a observar como as médias marginais (ajustadas) mudam em comparação às médias brutas. Parece que, após ajustar o modelo, as médias marginais foram maiores que as brutas nas condições manhã e tarde, mas foram menores que as médias brutas na condição noite.
Portanto, ao adotar médias marginais em análises estatísticas, os pesquisadores podem ter uma compreensão mais aprofundada e interpretável das relações, permitindo comparações mais precisas para nuances do conjunto de dados.
Conclusão
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Como citar este post
Lima, M. (2025, 14 de abril). O que são médias marginais? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-sao-medias-marginais/














