Neste post, você vai entender como a regressão linear pode ser usada para avaliar o poder preditivo de diferentes variáveis em contextos de pesquisa.
Primeiramente, introduzimos o funcionamento da regressão linear e sua aplicação na análise de relações entre variáveis. Em seguida, discutimos os diferentes termos utilizados na literatura, o que pode gerar confusão sobre seu uso.
Além disso, mostramos, por meio de um exemplo, os limites do modelo e os cuidados ao extrapolar previsões. Por fim, abordamos situações em que a regressão linear não é suficiente, indicando alternativas como a regressão logística.

Introdução ao poder preditivo da regressão linear
A regressão linear estabelece relações entre uma variável dependente contínua e uma ou mais variáveis independentes, conhecidas como preditoras. Dessa forma, usamos essas relações para prever ou explicar o comportamento da variável dependente.
Além disso, é um dos métodos mais populares em análises preditivas, sendo frequentemente comparado a técnicas como árvores de decisão e algoritmos de machine learning. Por esse motivo, muitos pesquisadores se referem à regressão como uma forma de análise preditiva.
Saiba mais: O que é machine learning?

A confusão nos termos e o impacto no entendimento
No entanto, um desafio comum é a variedade de termos usados na literatura estatística para descrever essa técnica. Diferentes autores adotam nomenclaturas distintas, o que pode ser confuso até mesmo para pesquisadores experientes. Portanto, compreender o real poder preditivo da regressão linear exige clareza conceitual.
Por exemplo, veja alguns dos termos mais comuns:
- Análise de regressão: é o nome mais genérico e amplamente utilizado, englobando tanto a regressão simples quanto a múltipla.
- Modelagem preditiva: aparece em contextos aplicados, como marketing e saúde, com foco explícito na previsão de resultados.
- Modelos lineares: enfatizam a estrutura matemática da regressão linear, sendo muito comuns em estatística clássica.
- Modelos lineares gerais (GLM): abrangem a regressão linear em sua forma matricial, incluindo variáveis contínuas e categóricas como preditores.
- Modelos de equações estruturais: em contextos como a psicometria, a regressão linear é frequentemente tratada como um caso particular desse tipo de modelagem.
- Análise multivariada: quando há múltiplos preditores, alguns autores categorizam a regressão múltipla dentro dessa abordagem.
Essas diferentes nomenclaturas, embora relacionadas, nem sempre são equivalentes. Assim, é essencial verificar como cada autor define os termos que utiliza para evitar confusões conceituais — principalmente ao interpretar o poder preditivo atribuído ao modelo.

Limitações do poder preditivo
Apesar de sua utilidade, o poder preditivo da regressão linear possui limitações importantes. Em primeiro lugar, devemos usar o modelo somente para prever dados que estejam dentro do intervalo observado na amostra original. Em segundo lugar, as previsões devem se restringir à população da qual a amostra foi retirada.
Ignorar essas recomendações pode levar a erros sérios de interpretação.
Exemplo prático: altura e peso
Considere o seguinte exemplo. Um médico coleta dados de altura (em cm) e peso (em kg) de 50 pacientes. Após ajustar um modelo de regressão linear simples, usando o peso como variável preditora e a altura como variável dependente, ele obtém a seguinte equação:
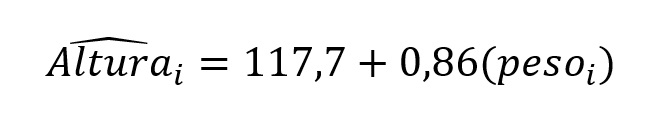
A Figura 1 mostra os dados desses 50 pacientes, acompanhada da reta de regressão, que representa a equação preditiva que mostramos anteriormente.

Desse modo, se um novo paciente pesa 70 kg, plugando esse valor na equação, o modelo prevê que ele terá 178 cm de altura:
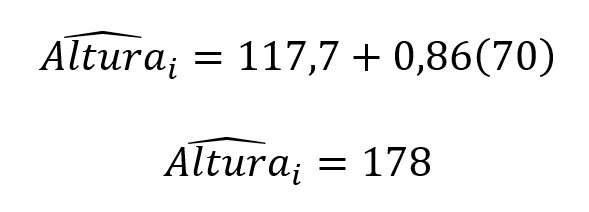
Desse modo, o modelo de regressão serve como ferramenta preditiva útil, desde que respeitados os limites dos dados originais — como veremos na seção seguinte.
Atenção aos limites da predição
É fundamental respeitar os limites empíricos de qualquer modelo. No exemplo da Figura 1, estimamos a equação da reta apenas com dados de pacientes entre 55 kg e 80 kg; logo, aplicar a mesma equação para alguém de 40 kg ou 100 kg é temerário, pois nada garante que a relação peso → altura continue linear fora desse intervalo.
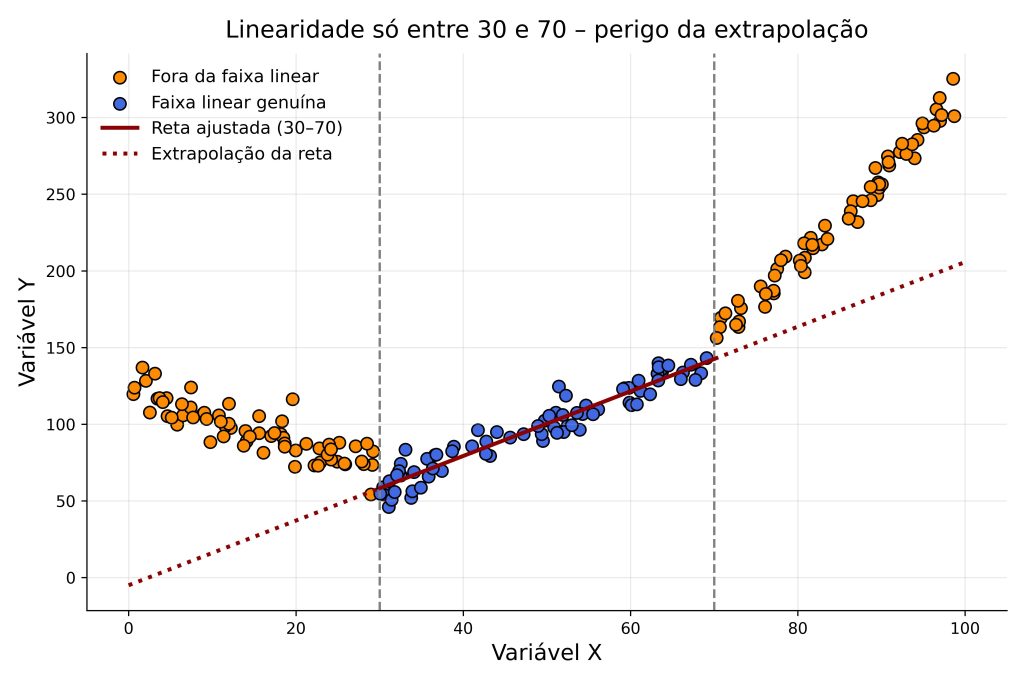
A Figura 2 reforça essa ideia em outro cenário, onde usamos duas variáveis genéricas, X e Y, onde X é a variável preditora e Y é a variável dependente.
Repare que:
- Pontos azuis (30 ≤ X ≤ 70) correspondem à amostra usada para ajustar a regressão; aqui a relação X → Y é realmente linear, e a reta sólida descreve bem os dados.
- Pontos laranjas (X < 30 ou X > 70) não fizeram parte do ajuste, isto é, consistem em dados que não foram observados em nossa amostra.
- A relação original, que se mostrou linear entre 30 e 70 é, na verdade, curvilinear quando consideramos todo o continuum da Variável X. Sendo assim, a mesma equação, prolongada como linha pontilhada vermelha, passa longe dos pontos observados—ou seja, gera previsões grosseiramente erradas.
A lição da Figura 2 é clara: um modelo linear só é válido dentro do domínio em que foi testado. Extrapolar para além dos valores amostrados compromete seriamente a exatidão preditiva.
Aplicações e extensões da regressão linear
De maneira geral, a regressão linear é útil para investigar o quanto um conjunto de variáveis consegue explicar um resultado específico. Por exemplo, podemos explorar o poder preditivo de subescalas de um teste de inteligência sobre o desempenho em uma tarefa.
Além disso, é possível testar se novas variáveis, como motivação, aumentam a capacidade explicativa do modelo. Assim, essa técnica oferece uma abordagem versátil para análises estatísticas.
Quando o poder preditivo da regressão linear não é suficiente
Entretanto, nem sempre devemos usar a regressão linear. Por exemplo, quando a variável dependente é categórica, técnicas como regressão logística binária (e.g., com vs. sem diagnóstico) ou multinomial (e.g., transtorno da personalidade borderline vs. histriônica vs. narcisista) são mais adequadas. Essas alternativas lidam melhor com variáveis qualitativas, preservando o rigor das análises preditivas.
Veja também: Diferença entre as regressões logísticas: binária, ordinal e multinomial

Conclusão
Gostou deste conteúdo? Então aproveite e também se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Como citar este post
França, A. (2022, 7 de junho). O que devo saber sobre o poder preditivo da regressão linear? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-devo-saber-sobre-o-poder-preditivo-da-regressao-linear/














