Modelagem por equações estruturais no R: conceitos e aplicações

A modelagem por equações estruturais é uma técnica de análise estatística que explica a relação entre variáveis latentes e observadas. Essa abordagem multivariada expande os princípios da regressão linear múltipla e da análise fatorial.

Neste post vamos falar sobre os conceitos e aplicações da modelagem por equações estruturais. Além disso, introduziremos a síntaxe da modelagem de equações estruturais no software e ambiente R.

Veja também: Introdução à modelagem por equações estruturais

Introdução à modelagem por equações estruturais

A modelagem por equações estruturais é uma técnica de análise multivariada, amplamente empregada nas ciências sociais e médicas. Suas aplicações são variadas, indo desde a análise de relações simples entre variáveis até análises complexas de equivalência de medição para construtos de primeira e ordens superiores.

Por sua estrutura ser flexível para o desenvolvimento e análise de relações complexas entre múltiplas variáveis, permite que os pesquisadores testem a plausibilidade de modelos teóricos com base em dados observados.

Vantagens da modelagem por equações estruturais

Diferentemente de outros modelos estatísticos, como a regressão linear, a modelagem por equações estruturais modela relações complexas com variáveis inter-relacionadas. Além disso, a modelagem por equações estruturais difere da regressão múltipla pelo fato de que os itens individuais podem contribuir para a construção do modelo. Dentro de um modelo de equações estruturais, estimam-se regressões simples, bem como regressões múltiplas, simultaneamente.

Além disso, a modelagem por equações estruturais possibilita o cálculo de efeitos diretos e indiretos. Por fim, modelagem por equações estruturais também fornece estimativas para efeitos diretos e indiretos entre variáveis e pode lidar com estimativas de parâmetros de modelos para dados ausentes.

Saiba mais: O que é regressão linear múltipla?

Limitações da modelagem por equações estruturais

Apesar de suas vantagens, a modelagem por equações estruturais necessita de um tamanho de amostra grande para obter estimativas confiáveis dos parâmetros do modelo.

Isso significa que dados oriundos de uma amostra pequena tendem a ter parâmetros menos confiáveis em comparação com dados oriundos de uma amostra maior.

A modelagem por equações estruturais também requer um modelo teórico bem especificado, incluindo as relações entre variáveis observadas e latentes, assim como entre preditores e variáveis de resultado.

Algumas dessas especificações são desafiadoras e, se não forem feitas corretamente, podem resultar em um ajuste inadequado do modelo. Por isso, é fundamental ter familiaridade com conceitos estatísticos, como variáveis latentes e observadas, além de dominar diferentes testes — regressão linear, regressão logística, análises fatoriais — e softwares estatísticos.

Principais conceitos da modelagem por equações estruturais

Em seguida, vamos ver alguns dos principais conceitos que estão envolvidos na modelagem por equações estruturais.

Variáveis latentes e observadas

Na modelagem por equações estruturais, variáveis latentes — também conhecidas como variáveis não observadas — são aquelas que não podem ser medidas diretamente. Elas são, portanto, inferidas a partir de variáveis observadas.

Exemplos de variáveis latentes são abundantes em psicologia, ciências sociais e educação, tais como inteligência e autoestima (psicologia), status socioeconômico e identidade de gênero (ciências sociais), ou motivação acadêmica e habilidades cognitivas (educação).

Por outro lado, as variáveis observadas, ao contrário das variáveis latentes, são medidas diretamente e são influenciadas pelas variáveis latentes. Por exemplo, as respostas aos itens de um instrumento de autorrelato ou às tarefas de um teste cognitivo são diretamente observadas no formulário on-line, ou na folha de papel onde os participantes respondem.

Assumimos, portanto, que, subjacentes a essas respostas, temos variáveis latentes que são os agentes causais, que explicam o porquê de diferentes respondentes terem padrões de respostas distintos.

Além disso, outras respostas podem ser consideradas, em si mesmas, variáveis observadas, sem uma variável latente subjacente. Por exemplo, a renda e o estado civil são consideradas variáveis observadas, pois não assumimos que existam variáveis latentes subjacentes ao padrão de respostas dos respondentes a esses itens em um questionário socioeconômico.

Diagramas de caminho e notações

O diagrama de caminho mostra as várias relações entre variáveis em um modelo de equação estrutural.

Quadrados ou retângulos representam variáveis observadas, enquanto círculos ou ovais representam variáveis latentes.

As setas entre as variáveis representam as relações hipotéticas entre elas, podendo essas relações ser diretas, onde uma variável influencia outra; ou bidirecionais, onde não especificamos a direção da relação entre variáveis — apenas assumimos que elas estão relacionadas.

A Figura 1 ilustra um diagrama de caminho simples — muito embora possamos representar modelos muito mais complexos com essa mesma estrutura gráfica.

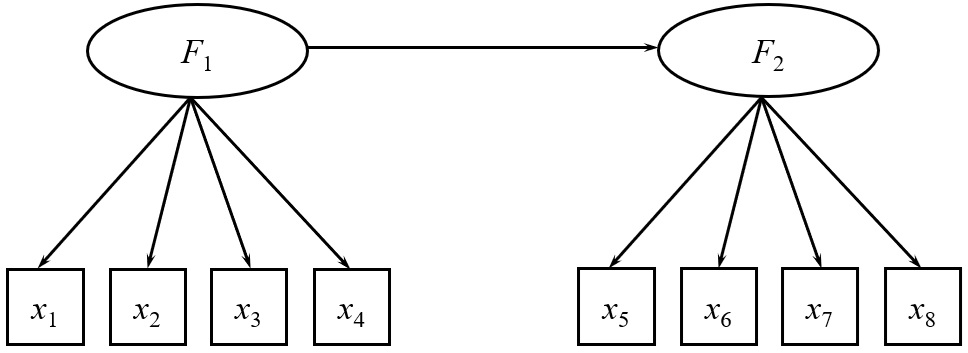
Na Figura 1, temos duas variáveis latentes (F₁ e F₂), onde assumimos que cada uma delas é responsável pelo padrão de respostas em quatro itens distintos. Além disso, assumimos uma relação causal entre as variáveis latentes, em que a variável latente F₁ influencia a variável latente F₂.

Variáveis endógenas e exógenas

Variáveis endógenas são variáveis hipotéticas causadas por outras variáveis no modelo. Estas são geralmente as variáveis dependentes no modelo. Na Figura 1, a variável F₂ é uma variável endógena.

Por outro lado, variáveis exógenas não são influenciadas por outras variáveis no modelo, mas, em vez disso, influenciam variáveis endógenas. Na Figura 1, a variável F₁ é uma variável exógena.

Variáveis endógenas geralmente têm setas apontando para elas (F₂, na Figura 1), enquanto variáveis exógenas, não (F₁, na Figura 1).

Na modelagem por equações estruturais, variáveis endógenas e exógenas podem ser tanto latentes quanto observadas.

Por exemplo, em um modelo que examina a relação entre felicidade e renda, a felicidade é modelada como uma variável latente com múltiplas variáveis observadas, como renda e estado civil.

A renda é uma variável endógena observada e diretamente medida no modelo, influenciada pela felicidade.

Efeitos diretos e indiretos

Para ilustrar os efeitos diretos e indiretos, veja a Figura 2.

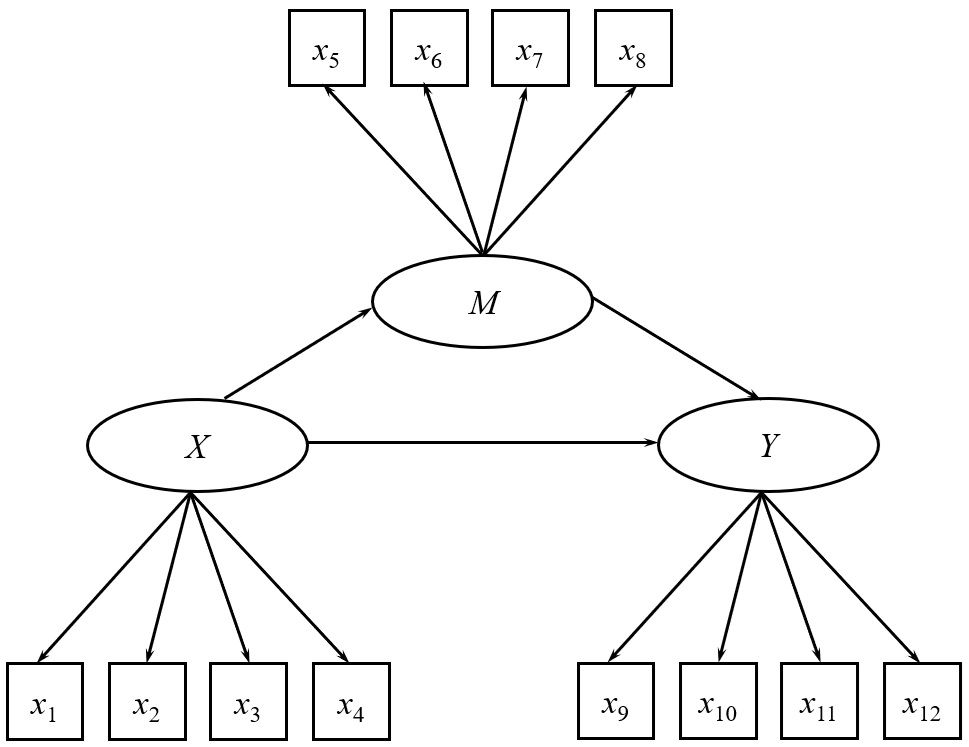
Um efeito direto é a relação direta entre duas variáveis, onde uma influencia a outra. Na Figura 2, os efeitos de X → Y, de X → M e de M → Y são efeitos diretos.

Por outro lado, um efeito indireto ocorre quando uma ou mais variáveis medeiam a relação no modelo. Na Figura 2, temos o efeito indireto X → M → Y, pois a variável mediadora M medeia a relação entre a variável exógena X e a variável endógena Y.

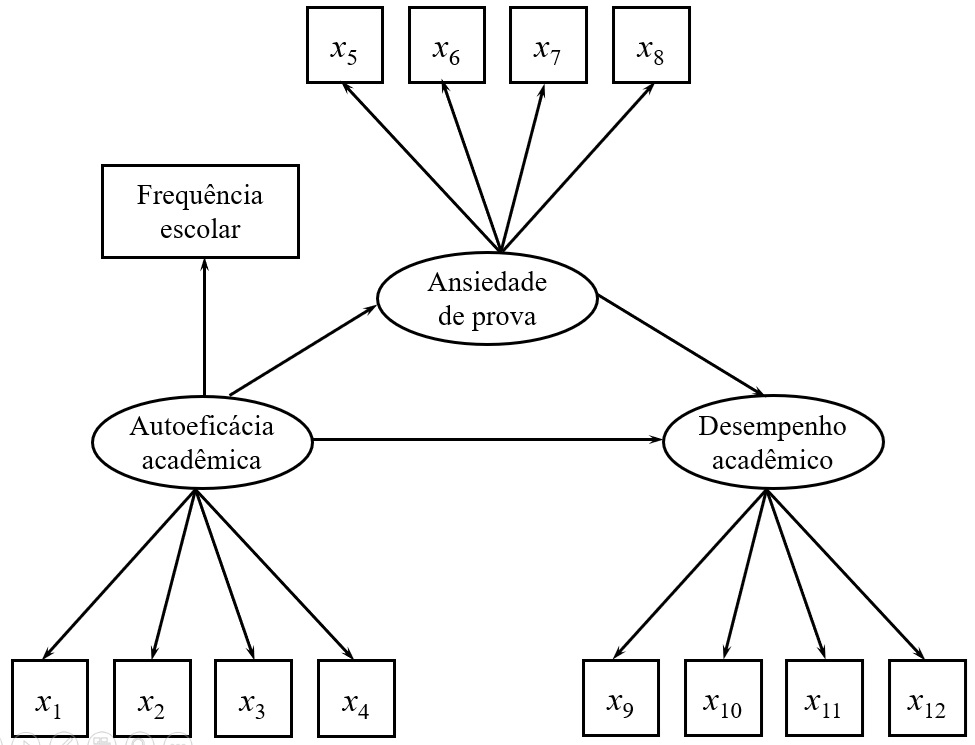
Por exemplo, na Figura 3, hipotetizamos que: (a) a autoeficácia acadêmica tem efeitos diretos sobre a frequência escolar, a ansiedade de prova e o desempenho acadêmico; (b) a ansiedade de prova tem um efeito direto sobre o desempenho acadêmico; e (c) a autoeficácia acadêmica tem um efeito indireto sobre o desempenho acadêmico através da variável mediadora ansiedade de prova.

Avaliação do modelo na modelagem por equações estruturais

Interpretando estimativas de parâmetros e erros-padrões

Estimativas de parâmetros são os valores dos coeficientes para cada variável preditora no modelo, isto é, elas explicam como a variável preditora afeta a variável de resultado.

Por exemplo, se a variável autoeficácia acadêmica apresenta um coeficiente de –4, isso indica que, a cada unidade de aumento na autoeficácia do estudante, espera-se uma redução de quatro faltas em sua frequência.

Erros-padrões são medidas de incerteza nas estimativas dos coeficientes. Em outras palavras, quanto menor o erro-padrão do coeficiente de uma variável, mais precisa é a estimativa do efeito daquela variável.

Interpretando índices de ajuste e testes de qualidade de ajuste

Para medirmos o ajuste de um modelo aos dados, podemos usar índices de ajuste e medidas de qualidade de ajuste. Esses índices incluem:

• Qui-quadrado: um valor não significativo indica um bom ajuste, embora às vezes não se possa confiar sempre no qui-quadrado devido à sua sensibilidade a grandes amostras. Ele provavelmente retornará um valor p significativo para um tamanho de amostra grande, independentemente da qualidade do ajuste do modelo.
• A razão do qui-quadrado pelos graus de liberdade (χ²/gl): preferencialmente, deve ser menor que 3.
• Erro quadrático médio de aproximação (RMSEA): consideramos um valor menor que 0,05 como um bom ajuste, enquanto um valor entre 0,05 e 0,08 indica um ajuste razoável. Valores acima de 0,10 são considerados um ajuste ruim.
• Índice de ajuste comparativo (CFI): um valor acima de 0,95 indica um bom ajuste, enquanto um valor abaixo de 0,90 indica um ajuste ruim.
• Índice Tucker–Lewis (TLI): um valor acima de 0,95 indica um bom ajuste, enquanto um valor abaixo de 0,90 indica um ajuste ruim.
• Resíduo quadrático médio padronizado (SRMR): consideramos um valor menor que 0,08 como um bom ajuste, enquanto um valor entre 0,08 e 0,10 indica um ajuste razoável. Valores acima de 0,10 indicam um ajuste ruim.

Interpretando resíduos e índices de modificação

Resíduos representam a diferença entre os valores observados e os valores previstos pelo modelo. Quanto menores esses resíduos, melhor o ajuste do modelo aos dados. Resíduos elevados podem indicar que o modelo está deixando de captar relações importantes, seja pela omissão de variáveis relevantes, por especificações inadequadas ou pela violação de suposições estatísticas.

Índices de modificação são estatísticas derivadas da matriz de resíduos que indicam quanto a qualidade do ajuste melhoraria se determinadas restrições do modelo fossem relaxadas — por exemplo, permitindo uma associação entre variáveis que não foi originalmente prevista no modelo teórico.

Embora esses índices ofereçam pistas úteis para a reespecificação do modelo, seu uso deve ser criterioso. Ao ajustar o modelo com base nessas sugestões post hoc, corre-se o risco de comprometer o caráter confirmatório da modelagem, aproximando-se de uma abordagem exploratória.

Aplicações da modelagem por equações estruturais

Modelagem por equações estruturais na psicologia

Na psicologia, os pesquisadores frequentemente buscam entender como diferentes fatores se relacionam entre si e como contribuem para comportamentos, emoções ou processos mentais.

A modelagem por equações estruturais ajuda a examinar essas relações complexas, criando um modelo que representa o quadro teórico do estudo.

Também podemos usar a modelagem por equações estruturais para testar a existência de variáveis latentes. Por exemplo, um pesquisador pode querer testar a relação entre ansiedade e desempenho acadêmico.

A modelagem por equações estruturais pode ajudar a identificar se variáveis latentes como ansiedade e motivação, podem influenciar, por exemplo, o desempenho acadêmico.

Modelagem por equações estruturais nas ciências sociais

Nas ciências sociais, os pesquisadores frequentemente buscam compreender como diferentes fatores contribuem para um determinado resultado. Por exemplo, podemos estar interessados em como as práticas parentais afetam o comportamento infantil ou em como o apoio social impacta a saúde mental.

A modelagem por equações estruturais permite aos pesquisadores criar um modelo que representa as relações hipotéticas entre esses fatores e, em seguida, testar se os dados apoiam esse modelo.

Além disso, também podemos usar a modelagem por equações estruturais para explorar relações mais complexas, como efeitos mediadores e moderadores. Efeitos mediadores ocorrem quando uma terceira variável explica a relação entre duas outras, isto é, a terceira variável consiste no mecanismo explicativo que faz a ligação causal entre duas outras variáveis. Em contrapartida, efeitos moderadores ocorrem quando uma terceira variável afeta a força ou a direção da relação entre duas variáveis.

Saiba mais: Análises de mediação e de moderação: definições e diferenças

Modelagem por equações estruturais na educação

Na educação, podemos aplicar a modelagem por equações estruturais para analisar vários aspectos da pesquisa educacional. Por exemplo, podemos investigar o impacto de diferentes métodos de ensino no desempenho dos estudantes, a eficácia de intervenções ou programas e as relações entre o treinamento de professores e os resultados de aprendizagem dos estudantes.

Uma aplicação prática da modelagem por equações estruturais na educação é ajudar a determinar as práticas instrucionais mais eficazes para melhorar o desempenho dos alunos. Os pesquisadores podem usar a modelagem por equações estruturais para analisar a relação entre diferentes métodos de ensino, características dos alunos e desempenho acadêmico.

Por exemplo, podemos investigar quais estratégias de ensino, como instrução direta ou aprendizado baseado em solução de problemas (problem-based learning), são mais eficazes para melhorar o desempenho dos alunos em diferentes disciplinas ou níveis de ensino.

Sintaxe da modelagem por equações estruturais usando o R

O que é lavaan?

O pacote lavaan, criado por Yves Rosseel, é uma ferramenta importante no ambiente de programação R para realizar a modelagem por equações estruturais.

Lançado em 2012, lavaan é um acrônimo para Latent Variable Analysis, refletindo seu foco em análises estatísticas que envolvem variáveis latentes.

A principal utilidade do lavaan é oferecer aos usuários do R uma maneira acessível e flexível de especificar e ajustar modelos de equação estrutural. Isso é particularmente útil em pesquisas que exploram relações complexas entre variáveis observáveis e não observáveis, como fatores psicológicos, sociais ou econômicos.

O lavaan se destaca por sua facilidade de uso, permitindo que mesmo aqueles com conhecimento estatístico moderado possam construir e analisar modelos de equação estrutural.

Entre suas principais funcionalidades, o lavaan permite realizar análises fatoriais confirmatórias (CFA), análises de caminho, modelos de variáveis latentes, além de calcular efeitos diretos, indiretos e totais entre variáveis.

No lavaan, utilizamos o operador til (~), tal como na regressão, lido como “é regredido em”. Nessa sintaxe, chamamos a variável dependente antes do til, e as variáveis independentes, após o til. Desse modo, definimos um modelo típico de caminho por um conjunto de fórmulas de regressão.

Instalando e carregando o lavaan

Podemos instalar e carregar o pacote por meio do código a seguir.

# instalando e carregando o pacote
install.packages("lavaan")
library(lavaan)

Devemos executar o código da linha 2 uma única vez. Por outro lado, devemos executar o código da linha 3 sempre que iniciarmos uma nova sessão no R.

Criando um objeto de modelo

O objeto de modelo é onde você especifica seu modelo para a análise. O código a seguir mostra um exemplo.

# criando um objeto de modelo
model <- "y =~ x1 + x2"

No código acima, o operador =~ especifica as variáveis observadas x1 e x2 para a variável latente y. Na especificação do modelo, podemos ainda usar outros operadores. Por exemplo, o operador ~ especifica uma regressão entre variáveis de resultado e preditoras, e ~~ especifica a covariância entre variáveis. Veja o exemplo a seguir.

# criando um novo objeto de modelo
model <- """
y =~ x1 + x2 
y ~ x3 + x4 
x3 ~~ x5
"""

No código anterior, x1 e x2 são variáveis observadas, influenciadas por y. A variável latente y também é predita por duas variáveis, x3 e x4. Além disso, especificamos uma relação de covariância entre x3 e x5.

Ajustando o modelo

Para ajustar um modelo de equação estrutural, você usa a função sem(), especificando o objeto do modelo e também os dados. No exemplo a seguir, my_data é um objeto qualquer que contém nosso banco de dados, e model é um dos modelos que especificamos anteriormente.

# ajustando o modelo aos dados
fit <- sem(model, data = mydata)

Extraindo os resultados do modelo

Os resultados são extraídos do modelo ajustado usando a função summary().

# extraindo os resultados do modelo
summary(fit, standardized = TRUE)

Compreender a sintaxe é apenas o início de uma jornada fascinante no mundo da análise multivariada. A habilidade de modelar e analisar relações complexas entre múltiplas variáveis abre portas para insights mais profundos e conclusões mais fundamentadas em suas pesquisas.

Conclusão

Este post introduziu conceitos e aplicações da modelagem por equações estruturais. Além disso, mostramos como aplicar a modelagem por equações estruturais no R. Se você utiliza modelagem por equações estruturais em suas pesquisas, mas ainda não é um usuário do R, então veja a novidade que preparamos a seguir!

É com grande satisfação que a Psicometria Online anuncia o curso R para Iniciantes. O curso tem como objetivo abordar todos os tópicos essenciais do R, permitindo, portanto, que você explore assuntos específicos sem ser prejudicado por dúvidas básicas. Se você trabalha com pesquisa científica e deseja aprender a utilizar o R, então o curso R para Iniciantes é para você.

Além disso, se você quer saber mais sobre a Psicometria Online Academy, acesse nosso site. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).

Referências

Beran, T. N., & Violato, C. (2010). Structural equation modeling in medical research: A primer. BMC Research Notes, 3, Article 267. https://doi.org/10.1186/1756-0500-3-267

Kline, R. B. (2016). Principles and practice of structural equation modeling (4^th ed.). The Guilford Press.

Como citar este post

França, A. (2025, 29 de abril). Modelagem por equações estruturais no R: Conceitos e aplicações. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/modelagem-por-equacoes-estruturais-no-r-conceitos-e-aplicacoes/