Em teoria da medida, a confiabilidade (ou fidedignidade) se refere à consistência das mensurações em diferentes condições. A fim de estimar a confiabilidade dos escores obtidos em pesquisas, psicometristas desenvolveram vários métodos. Neste post, nosso objetivo é apresentar a confiabilidade por duas metades. Além disso, também descreveremos como calculá-la e quais são suas principais limitações.
O que é confiabilidade por duas metades?
A confiabilidade por duas metades (split-half reliability) é um método estatístico que avalia a consistência interna dos escores de um instrumento de mensuração. Em outras palavras, ela avalia em que medida os itens de uma tarefa ou instrumento avaliam consistentemente o mesmo construto ou traço latente.
Por exemplo, na tarefa de Stroop, os participantes veem palavras representando nomes de cores. Essas palavras são exibidas em diferentes cores (e.g., palavra AZUL na cor azul). Os participantes devem identificar, rápida e precisamente, a cor da palavra, ou seja, ignorando o texto apresentado (Figura 1).

Suponha que cada participante realizou 500 tentativas na tarefa de Stroop. Nesse caso, queremos estimar a confiabilidade do desempenho dos participantes na tarefa de Stroop.
Eis um exemplo envolvendo instrumento de autorrelato: o Brief Loquaciousness and Interpersonal Responsiveness Test (BLIRT) é um teste, composto por oito itens, que avalia em que medida uma pessoa responde às demais de forma rápida e efusiva (e.g., “Se eu tenho algo a dizer, não hesito em dizer”). Os respondentes avaliam os itens em uma escala de cinco pontos, de 1 (Discordo totalmente) a 5 (Concordo totalmente).
Ao aplicar a técnica da confiabilidade por duas metades, estimamos a consistência interna de metade dos escores do instrumento. A fim de estimarmos a consistência do teste como um todo, aplicamos um fator de correção à estimativa original.

Como calcular a confiabilidade por duas metades?
Em seguida, mostraremos as etapas envolvidas no cálculo da confiabilidade por duas metades.
Coletando dados
Primeiramente, coletamos dados. Por exemplo, podemos aplicar a tarefa de Stroop ou um instrumento de autorrelato (BLIRT) em uma amostra de participantes.
Dividindo os itens da tarefa ou instrumento em duas metades
Em seguida, dividimos os itens da tarefa ou instrumento em duas metades equivalentes. Por exemplo, no caso da tarefa de Stroop, a primeira metade da tarefa poderia representar um subconjunto de itens, enquanto a segunda metade da tarefa poderia representar outro subconjunto (Figura 2).

Já no caso do BLIRT, poderíamos dividir os itens em ímpares e pares (Figura 3).

Pontuando as duas metades
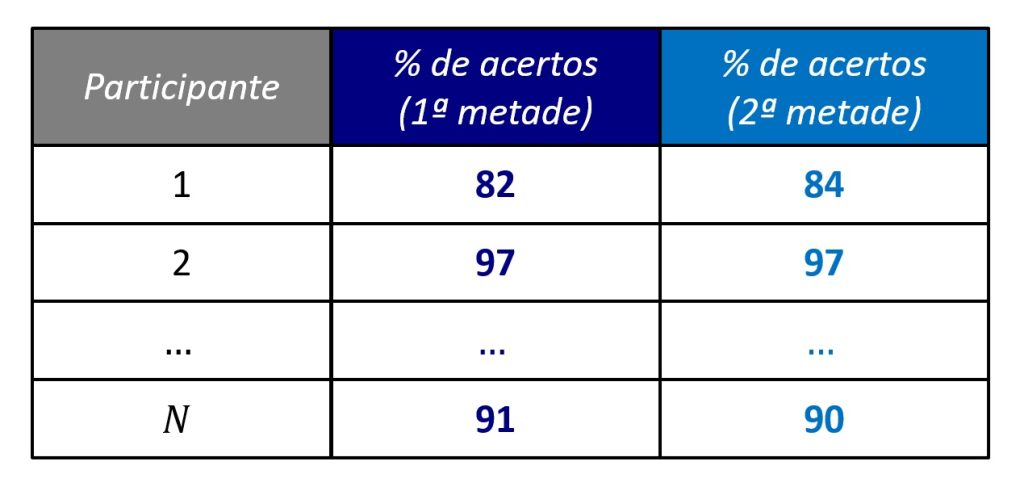
Depois disso, precisamos pontuar cada metade dos itens, para cada participante. Por exemplo, na tarefa de Stroop, podemos calcular, para cada participante da amostra, o percentual de acertos na primeira metade e na segunda metade da tarefa de Stroop. Desse modo, nosso banco de dados terá duas colunas adicionais, conforme ilustra a Figura 4.
No caso de instrumentos de autorrelato, é importante que todos os itens tenham a mesma orientação. Por exemplo, no caso do BLIRT, o item “Se eu tenho algo a dizer, não hesito em dizer” é positivamente orientado, pois alguém com maior propensão a ser responsivo aos outros tenderá a concordar mais com essa afirmação.
Em contrapartida, o item “Frequentemente, levo um tempo para descobrir como me expressar” é negativamente orientado, pois alguém com maior propensão a ser responsivo aos outros tenderá a discordar mais dessa afirmação.
No BLIRT, os itens 2, 3, 5, 7 e 8 são pontuados de forma reversa. Desse modo, precisamos ajustá-los para que eles fiquem na mesma direção que os demais itens. A solução é simples: basta calcular escoreajustado = 6 – escoreoriginal para os itens com orientação reversa, de modo a ancorarmos todos os itens na mesma direção.
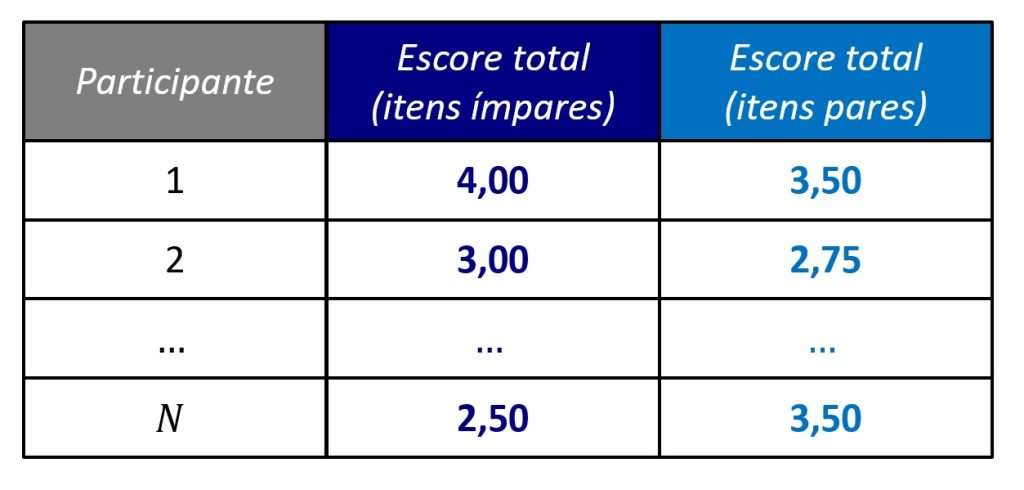
Em seguida, calculamos o escore total do BLIRT para as duas metades. Podemos calcular o escore total com base na soma ou na média dos itens que compõem cada metade. Na Figura 5, ilustramos o cálculo usando a média.
Calculando a confiabilidade por duas metades
Na próxima etapa, calculamos o coeficiente de correlação entre os escores obtidos nas duas metades. Tipicamente, usamos técnicas como as correlações de Pearson ou de Spearman para essa finalidade.
Por exemplo, usando o banco de dados de Hayes e Coutts (2020), calculamos os escores totais com base nos itens ímpares e pares, separadamente, e, para fins ilustrativos, plotamos esses escores na Figura 6.

A Figura 6 sugere uma relação linear positiva entre os escores totais ímpares e pares, o que seria esperado em uma situação em que há confiabilidade dos escores. Essa impressão visual é corroborada estatisticamente por meio do cálculo da correlação entre as duas metades do instrumento, r = 0,65.
Aplicando a correção de Spearman–Brown à estimativa de confiabilidade por duas metades
Contudo, não estamos interessados na confiabilidade da metade do instrumento, mas sim na confiabilidade do instrumento como um todo. Para esse fim, usamos a a correção de Spearman–Brown (ou fórmula da profecia de Spearman–Brown), uma correção que visa predizer qual seria a correlação se o nosso teste tivesse outro comprimento.
A correção de Spearman–Brown é dada por:
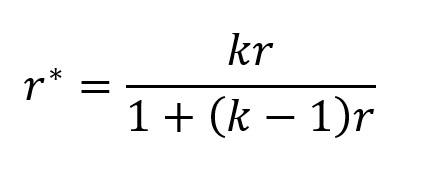
onde k representa a razão entre o número de itens no instrumento novo e no instrumento original, r representa a correlação original entre as duas metades e r* representa a correlação prevista com a mudança no número de itens.
No caso particular em que usamos a correção de Spearman–Brown na confiabilidade por duas metades, queremos estimar a confiabilidade para o dobro da metade dos itens (i.e., para o instrumento completo). Logo, k = 2. Aplicado aos nossos dados, temos:
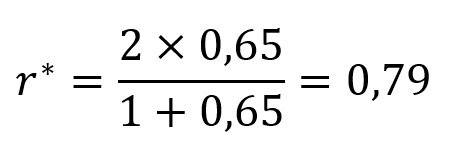
Desse modo, nossa estimativa de consistência interna com base no método da confiabilidade por duas metades é de r = 0,79. Uma vez que esse valor é maior que 0,70, concluiríamos que nossa estimativa de confiabilidade foi aceitável.
Limitações da confiabilidade por duas metades
Anteriormente, dissemos que o método da confiabilidade por duas metades exige que os itens da tarefa ou instrumento sejam divididos em duas metades equivalentes. No entanto, demos pouca atenção ao termo em negrito, de modo que as divisões que sugerimos (i.e., 1ª metade vs. 2ª metade; itens ímpares vs. itens pares) foram um tanto arbitrárias.
De fato, uma das críticas do método consiste na dificuldade em garantir a equivalência entre as duas metades. Considere, por exemplo, a tarefa de Stroop: suponha que, devido à longa duração da tarefa, os participantes se cansem na segunda metade do teste.
Nesse caso, as estimativas de confiabilidade serão atenuadas porque não há equivalência entre os desempenhos nas duas metades da tarefa. Um problema análogo ocorreria, por exemplo, em testes cognitivos (e.g., de inteligência) em que a dificuldade dos itens é crescente ao longo da tarefa.
Em segundo lugar, é difícil determinar como devemos dividir os itens para aplicar a técnica da confiabilidade por duas metades. Por exemplo, no caso do BLIRT, com oito itens:

Isto é, existem 35 formas distintas de dividirmos os oito itens do BLIRT em duas metades. Mais importante, diferentes divisões podem retornar estimativas de confiabilidade distintas. Por exemplo, a Figura 7 apresenta a distribuição de estimativas para as 35 duas metades possíveis do BLIRT, que variaram entre 0,67 e 0,83.
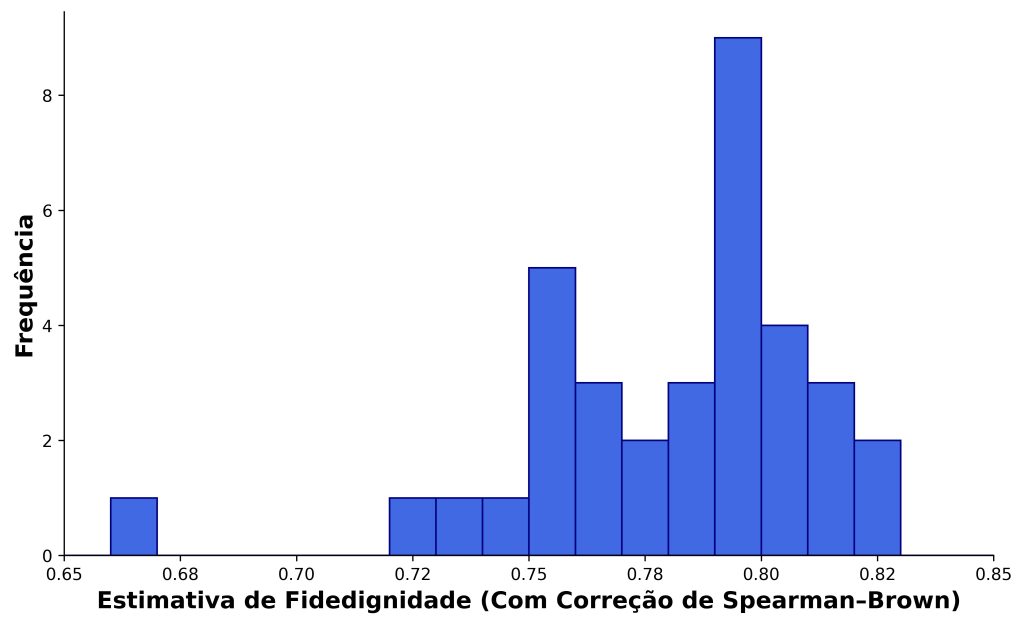
Desse modo, pode ser problemático se basear apenas em uma estimativa que depende do método de divisão dos itens. Portanto, embora a confiabilidade por duas metades possa ser uma ferramenta útil para avaliar a consistência interna de tarefas e de instrumentos, os investigadores devem ter ciência de suas limitações.
Conclusão
Neste post, você aprendeu sobre a confiabilidade por duas metades, como calculá-lá e quais suas limitações. Esperamos que o conteúdo do post tenha sido útil!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Hayes, A. F., Coutts, J. J. (2020). Use omega rather than Cronbach’s alpha for estimating reliability. But… Communication Methods and Measures, 14(1), 1–24. https://doi.org/10.1080/19312458.2020.1718629
Pasquali, L. (2003). Psicometria: Teoria dos testes na psicologia e na educação. Editora Vozes.
Zanon, C., & Hauck-Filho, N. (2015) Fidedignidade. In C. S. Hutz, D. R. Bandeira, & C. M. Trentini (Orgs.), Psicometria (pp. 85–96). Artmed.
Como citar este post
Lima, M. (2025, 1 de janeiro). Compreendendo a confiabilidade por duas metades (split-half reliability). Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/compreendendo-a-confiabilidade-duas-metades-split-half-reliability/














