Neste post, você aprenderá a criar gráficos no R com o ggplot2.
Por que criar gráficos no R?
Você provavelmente já ouviu a expressão “uma imagem vale mais que mil palavras”. Em pesquisas científicas, por exemplo, um gráfico bem construído ajuda pesquisadores a comunicarem mensagens poderosas sobre os resultados de suas pesquisas.
Desse modo, este post objetiva apresentar um pacote do R especializado na construção de visualizações gráficas elegantes, personalizadas e de alta qualidade. Desse modo, tais características do pacote justificam o uso do R para criar gráficos para seus relatos científicos.
O que é o ggplot2?
Em um post anterior, introduzimos o R, um ambiente e uma linguagem de programação cujos focos principais incluem a manipulação, a análise e a visualização de dados. Criado em 2005, o pacote ggplot2 se baseia nas ideias de Leland Wilkinson expostas no livro The Grammar of Graphics.
O princípio básico do pacote ggplot2 é que gráficos podem ser construídos usando uma abordagem multicamadas. Em outras palavras, um gráfico pode ser decomposto em diferentes camadas que, quando sobrepostas, geram a impressão visual daquilo que chamamos de “gráfico”. Desse modo, o usuário pode inserir camadas distintas e independentes em seus gráficos no R, de modo a obter a saída final que atenda às suas necessidades.
A Figura 1 ilustra a abordagem multicamadas de um gráfico segundo a filosofia do ggplot2.

ggplot2. A Figura 1 indica que um gráfico pode ser composto pelos dados, sobre os quais é aplicada alguma estética, isto é, propriedades visuais, que incluem forma, tamanho, cores de contorno e de preenchimento, para citar algumas delas.
Outras camadas incluem, por exemplo, as propriedades dos eixos onde as informações serão plotadas, propriedades do tema (estilo do gráfico) e da legenda (posição, título e demais características). Além disso, camadas adicionais podem ser inseridas nos gráficos. Se combinamos diferentes camadas gráficas, então o resultado é indicado pela representação final no painel à direita da Figura 1.
Evidentemente, quando começarmos a criar gráficos no R, poderemos combinar as camadas de formas distintas, a depender, contudo, do propósito da representação visual. Por exemplo, diferentes geometrias são aplicáveis a representações visuais distintas. O ggplot2 possui, permite criar histogramas (geom_histogram()), diagramas de dispersão (geom_point()) e gráficos de linhas (geom_lines()), para citar três exemplos.
Mostraremos, a seguir, como criar seus primeiros gráficos no R. Inicialmente, plotaremos um gráfico com parâmetros default para, em seguida, inserirmos algumas customizações. Desse modo, seremos capaz de introduzir a você o poder do R em produzir representações gráficas elegantes e eficientes.
Como instalar e carregar o pacote ggplot2?
Primeiramente, é importante instalar e carregar o pacote usado no tutorial. No entanto, reforçamos que a instalação (linha 2) deverá ser feita apenas uma vez, enquanto o carregamento do pacote (linha 3) deverá ser feito sempre que você iniciar uma nova sessão no R. O bloco de códigos a seguir mostra como realizar essas duas operações.
# instalando e carregando o pacote ggplot2
install.packages("ggplot2")
library(ggplot2)
Criando dados sintéticos no R (Parte 1)
Para explorar o poder do R na visualização de dados, no entanto, precisaremos de dados disponíveis. Se você possui dados de sua própria pesquisa, então eles podem ser usados para esse fim. No entanto, aqui criaremos dois conjuntos fictícios de dados, pois eles atendem a algumas características interessantes para o nosso tutorial.
O primeiro conjunto de dados (dados1) contém três variáveis, sendo duas delas contínuas (x e y) e uma delas categórica (grupo, dividido em A e B). A variável y foi criada para ter distribuições ligeiramente distintas para cada grupo.
# define semente para reprodutibilidade
set.seed(42)
# tamanho amostral
N <- 2000
# variável com distribuição normal
x <- rnorm(n = N)
# variável com distribuição distinta para os grupos A e B
y <- c(x[1: (N / 2)] + rnorm(N / 2),
3 + x[(N / 2 + 1):N] + rnorm(N / 2))
# variável de grupo
grupo <- rep(c("A", "B"), each = N / 2)
# insere todas as variáveis em um dataframe
dados1 <- data.frame(x = x,
y = y,
grupo = grupo)
A Figura 2 apresenta as 10 primeiras linhas de dados1.
# apresenta as 10 primeiras linhas
head(dados1, 10)

dados1. Deixaremos, contudo, para apresentar o segundo conjunto de dados mais adiante.
Como criar histogramas no R com o ggplot2?
Criando um histograma básico no R
Vamos iniciar nossos exemplos com o histograma, uma representação gráfica que é útil, por exemplo, para avaliarmos a distribuição dos dados. Para inicializar nosso gráfico, usaremos a função ggplot, do pacote ggplot2. (Note que o termo ggplot2, com o “2” no final, refere-se ao pacote, enquanto o termo ggplot, sem o “2” no final, refere-se à função daquele mesmo pacote.)
O primeiro gráfico é criado por meio do código a seguir:
# gráfico 1
ggplot(dados1,
aes(x)) +
geom_histogram()
Vamos resumir o que o código anterior faz:
- Na linha 25, passamos nosso dataframe
dados1à funçãoggplot; - Dentro da função
ggplot, usamos a funçãoaes(), passando as variáveis sobre as quais queremos aplicar algumas características estéticas. Podemos especificar, por exemplo, qual variável será plotada no eixo x e qual será plotada no eixo y, ou mesmo definir se as cores de contorno e de preenchimento de uma variável irá variar em função de outra variável; - A função
geom_histogram()cria um objeto geométrico que representará o histograma da colunaxno dataframedados1.
A Figura 3 apresenta o histograma gerado pelo código anterior.
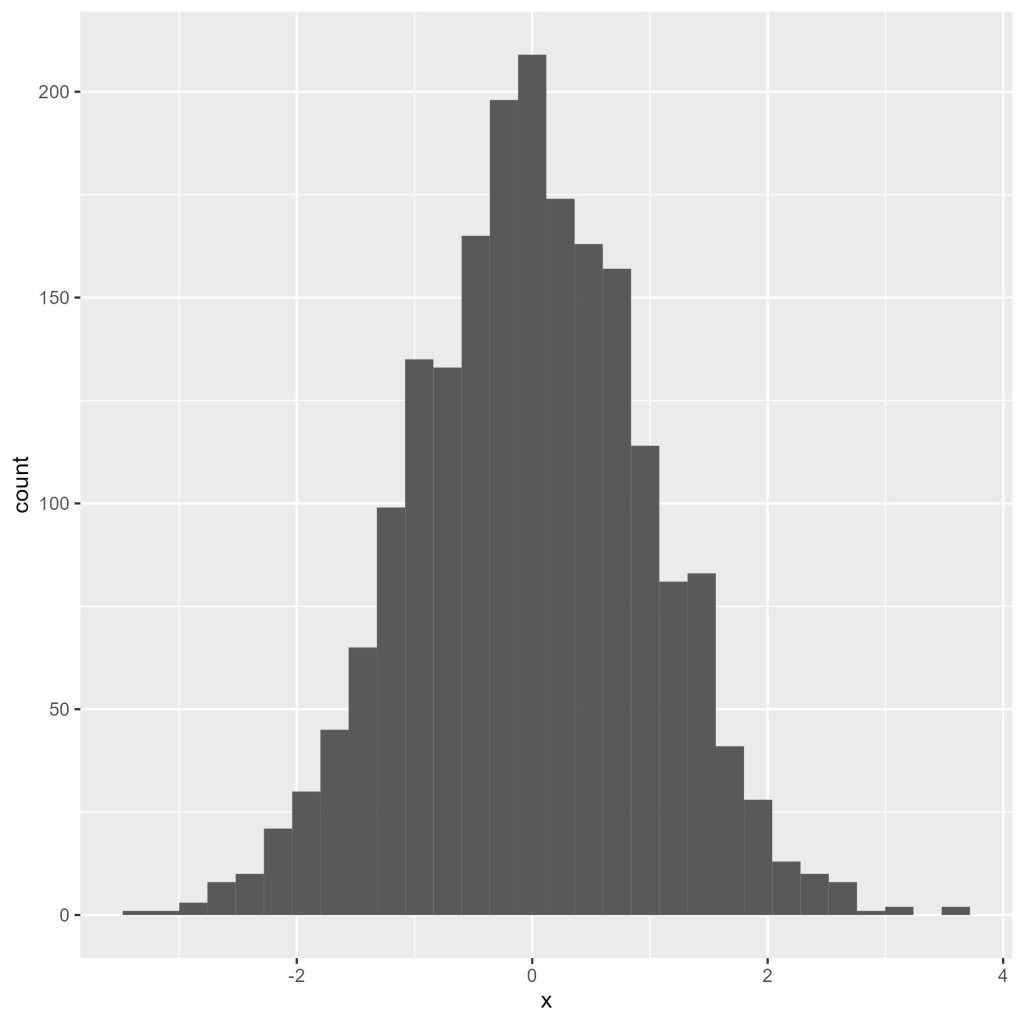
Criando histogramas personalizados no R
Se o usuário não passa parâmetros adicionais às funções que compõem as diferentes camadas do gráfico, então teremos gráficos com valores default definido pelos criadores do pacote. Por exemplo, como não definimos a cor do histograma, o gráfico apresentado aparece na cor cinza. Contudo, visando melhorar a apresentação gráfica do histograma, o bloco de códigos a seguir customiza as propriedades do histograma.
# gráfico 2
ggplot(dados1,
aes(x)) +
geom_histogram(binwidth = 0.3,
color = "black",
fill = "lightblue")
No código anterior, acrescentamos três argumentos em geom_histogram():
- Argumento
binwidth(linha 32): define a largura de cada barra do histograma. Valores menores indicam barras mais estreitas; - Argumento
color(linha 33): define a cor de contorno das barras do histograma; - Argumento
fill(linha 34): define a cor de preenchimento das barras do histograma.
A Figura 4 apresenta o gráfico gerado pelo código anterior.

Considere, por exemplo, que queremos que as barras do histograma tenham cores distintas para os dois grupos do banco de dados. A seguir, visando atingir esse objetivo, acrescentamos o parâmetro fill em aes(). Na prática, o R irá gerar histogramas separados para os grupos A e B. Além disso, definimos a transparência das barras (linha 41), bem como as cores das barras por grupo (linhas 42 e 43).
# gráfico 3
ggplot(dados1, aes(x,
fill = grupo)) +
geom_histogram(binwidth = 0.3,
color = "black",
alpha = 0.5) +
scale_fill_manual(values = c("A" = "red",
"B" = "darkblue")
)
A Figura 5 apresenta o gráfico resultante.
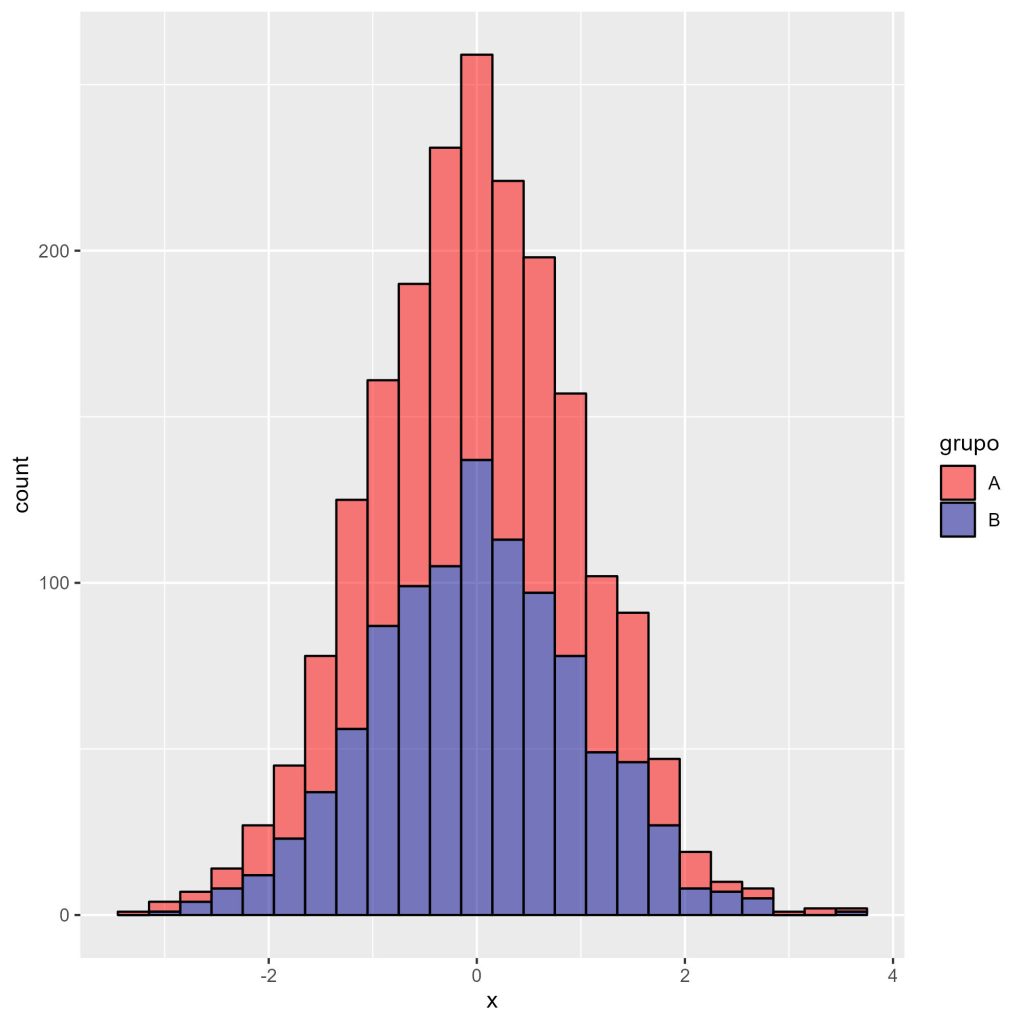
Como construir gráficos de densidade no R com o ggplot2?
Criando um gráfico de densidade básico no R
Um gráfico de densidade consiste em uma tentativa de aproximação da distribuição com base nos dados observados. Além disso, ele também fornece uma estimativa das características da distribuição. Em nosso primeiro gráfico de densidade, substituímos geom_histogram() por geom_density().
# gráfico 4
ggplot(dados1, aes(x)) +
geom_density()
A Figura 6 apresenta o gráfico de densidade resultante.
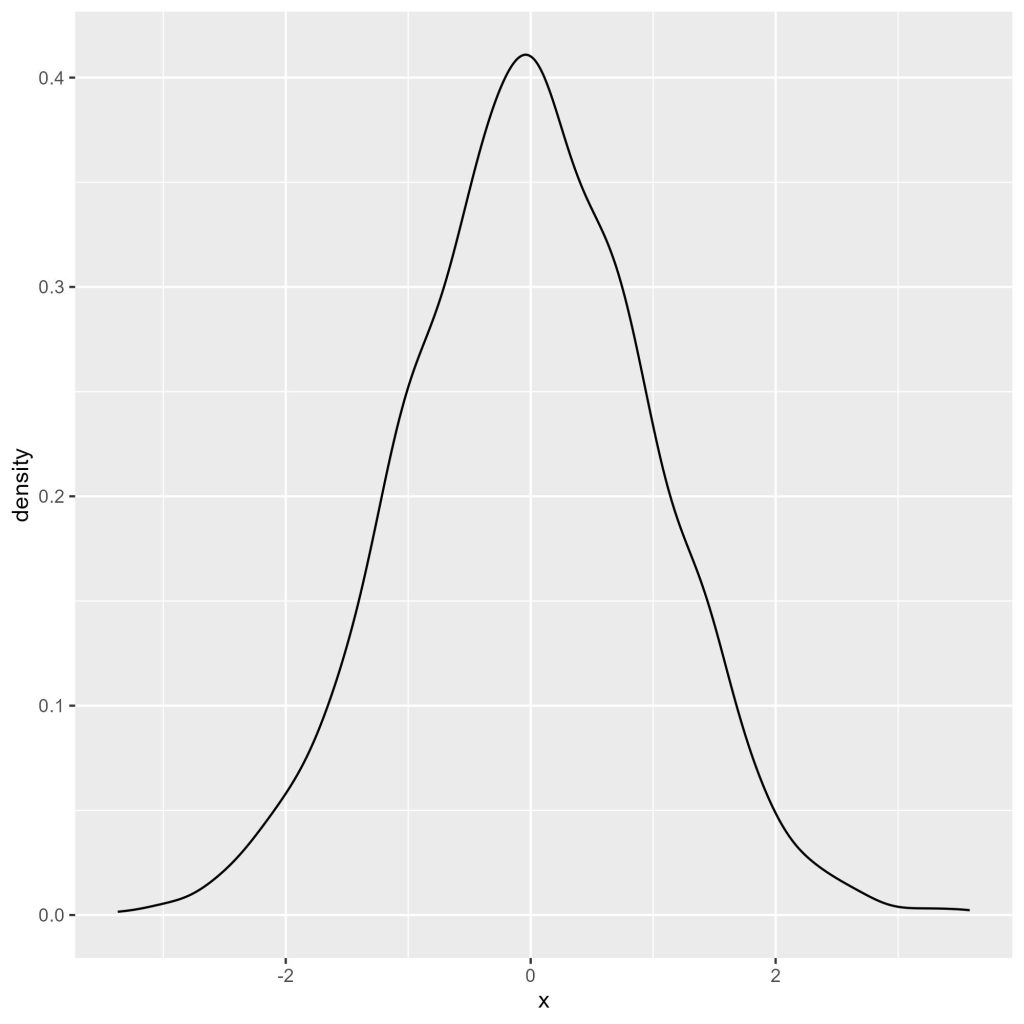
Criando gráficos de densidade personalizados no R
Podemos melhorar a apresentação do gráfico de densidade anterior, definindo a espessura (linha 52), a transparência (linha 53) e a cor da linha do gráfico (linha 54). A Figura 7 apresenta o gráfico gerado pelo código a seguir.
# gráfico 5
ggplot(dados1, aes(x)) +
geom_density(linewidth = 0.8,
alpha = 0.5,
color = "darkgreen")

Assim como fizemos com o histograma, podemos querer comparar diagramas de densidade entre grupos. Para isso, acrescentamos em aes(), o argumento grupo, tanto para color quanto para fill, indicando que queremos que os diagramas tenham cores de contorno e de preenchimento, respectivamente, distintas entre grupos A e B.
# gráfico 6
ggplot(dados1, aes(x = y,
color = grupo,
fill = grupo)) +
geom_density(linewidth = 0.8,
alpha = 0.5)
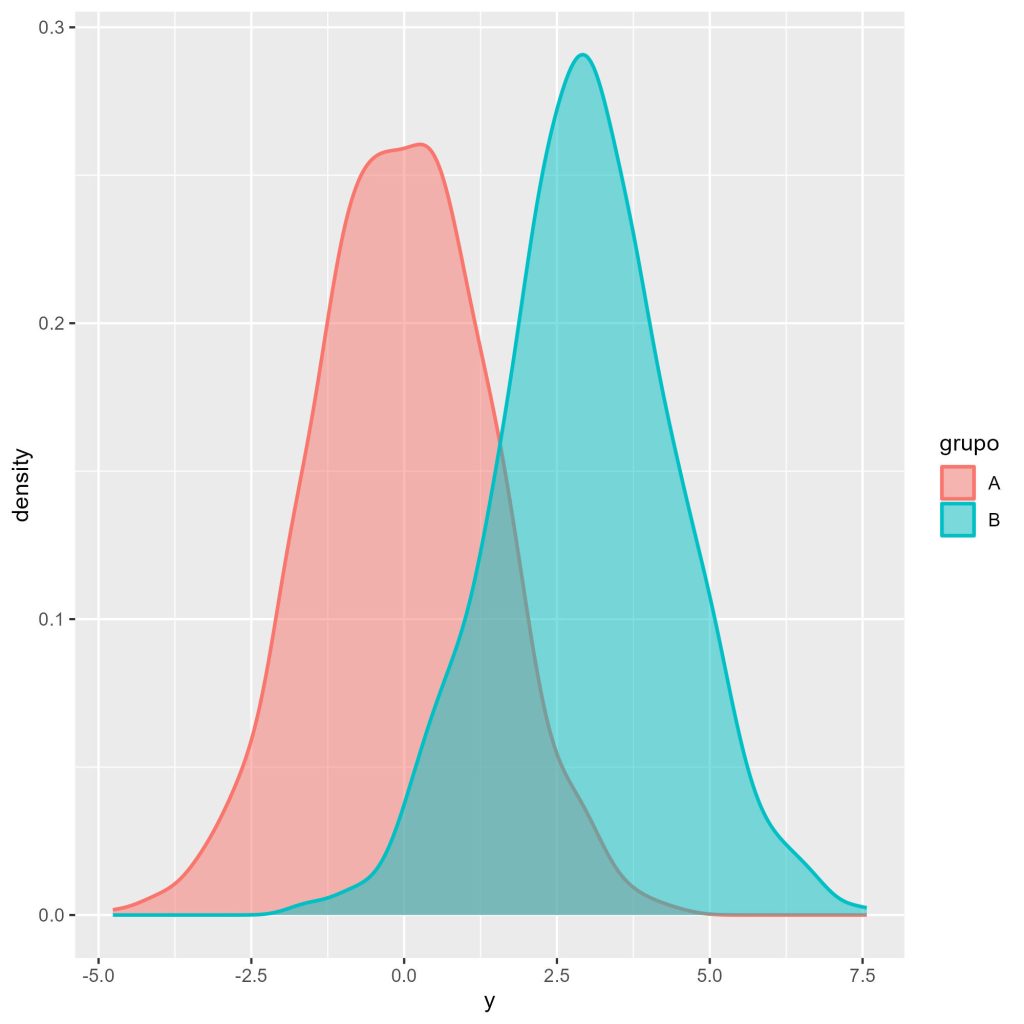
No gráfico anterior, a variável y parece ter distribuição aproximadamente normal para os dois grupos, mas tendo valores superiores para o grupo B (isto é, mais à direita do gráfico), em comparação ao grupo A.
Como criar boxplots no R com o ggplot2?
Criando um boxplot básico no R
O boxplot, também denominado de diagrama de caixas (ou diagrama de caixas e bigodes) também é um gráfico útil para mostrar características da distribuição, como quartis 1, 2 (mediana) e 3 e outliers.
No ggplot2, a geometria que permite gerar um boxplot é o geom_boxplot(). No código a seguir, geramos um único boxplot da variável y. Também definimos os limites do eixo x em xlim(), de modo a gerar um boxplot menor na área de plotagem.
# gráfico 7
ggplot(dados1, aes(y = y)) +
geom_boxplot() +
xlim(-1, 1)

Na Figura 9, a caixa representa a amplitude interquartílica, onde estão 50% das observações. A linha grossa interna da caixa representa a mediana, enquanto as linhas (os “bigodes”) representam 1,5 multiplicado pela amplitude interquartílica. Desse modo, valores para além dos limites dos bigodes podem ser considerados outliers. Em resumo, existe pelo menos um valor extremo negativo no gráfico, sinalizado pelo ponto preto na parte inferior do boxplot.
Criando boxplots personalizados no R
No código a seguir, dividimos o boxplot em função dos grupos. Além disso, acrescentamos mais uma camada ao boxplot. A geometria geom_jitter() permite plotar os pontos de dados. No entanto, alguns pontos podem ter sobreposição. Por isso, podemos acrescentar um ruído horizontal e/ou vertical aos pontos, de modo a evitar tais sobreposições.
Note que aqui a ordem importa: a camada plotada posteriormente no código causará a oclusão visual (parcial ou total) da camada plotada antes no código. Por exemplo, nós a seguir invocamos geom_jitter() antes que geom_boxplot(), pois queremos que os pontos apareçam atrás do boxplot.
Por fim, alteramos as cores de contorno (linha 77) e de preenchimento do boxplot (linha 78) e excluímos os destaques de outliers (linha 79), pois as observações já estão sendo plotadas com geom_jitter(). A Figura 10 apresenta o resultado do código a seguir.
# gráfico 8
ggplot(dados1, aes(x = grupo,
y = y)) +
geom_jitter(width = 0.3,
height = 0,
shape = 21,
alpha = 0.5,
size = 2,
color = "gray30") +
geom_boxplot(color = "mediumorchid4",
fill = "mediumorchid2",
outlier.shape = NA)

No próximo gráfico, substituíremos geom_jitter() por geom_errorbar(). O objetivo dessa nova geometria é modificar a aparência dos “bigodes” do boxplot, para que eles tenham formato de letra T. Além disso, também modificamos as cores dos boxplots (linhas 86 e 87), e acrescentamos um quadrado dentro das caixas (linhas 88 e 89) para representar as médias dos grupos no gráfico. A Figura 11 apresenta o resultado do código a seguir.
# gráfico 9
ggplot(dados1, aes(x = grupo,
y = y)) +
geom_errorbar(stat = "boxplot", # insere camada de barra de erro, para melhorar estética
width = 0.2) + # define largura dos limites das barras
geom_boxplot(color = "darkred", # modifica cores de contorno
fill = "tomato") + # e de preenchimento dos boxplots
stat_summary(fun = mean, # plota médias dos grupos
shape = 15) # como quadrados

Com base na figura anterior, notamos que a variável y parece ter distribuição aproximadamente normal nos dois grupos (denotadas por caixas e bigodes simétricos ao redor da mediana, bem como pela média tendo valor próximo à mediana). No entanto, dentro de cada grupo, parecem existir alguns outliers negativos e positivos, que podem necessitar de exploração adicional, antes de proceder a análises estatísticas inferenciais.
Como construir diagramas de dispersão no R com o ggplot2?
Criando um diagrama de dispersão básico no R
Enquanto os gráficos anteriores são úteis para mostrar como a distribuição de uma variável contínua difere ou não em função de uma variável categórica, diagramas de dispersão são úteis para investigar a relação entre duas variáveis contínuas. Esses gráficos bem comuns, por exemplo, em análises de correlação.
Para criarmos um diagrama de dispersão básico, informamos para aes() qual variável deve ser plotada no eixo x e qual variável deve ser plotada no eixo y. Em nosso caso, os nomes das variáveis (após o símbolo de igual) coincidem com os nomes dos parâmetros (antes do símbolo de igual), mas raramente esse será o caso em aplicações reais.
Por fim, para especificarmos nosso diagrama de dispersão, usamos uma camada que invoca a geometria geom_point(), inicialmente vazia. A Figura 12 apresenta o gráfico gerado pelo código a seguir.
# gráfico 10
ggplot(dados1, aes(x = x, # variável no eixo x
y = y)) + # variável no eixo y
geom_point()

Criando diagramas de dispersão personalizados no R
A Figura 12 sugere que as variáveis x e y estão positivamente correlacionadas. Mas será que esse padrão é similar para os grupos A e B? Para inspecionar a relação bivariada de x e y em função de grupo, informamos à função aes() que a cor dos pontos deve ser distinta a depender do grupo de cada observação (linha 99). A Figura 13 apresenta o gráfico resultante.
# gráfico 11
ggplot(dados1, aes(x = x,
y = y,
color = grupo)) +
geom_point()

Agora notamos que a relação entre as variáveis parece ser similar para os dois grupos, embora o grupo B tenha escores em média mais elevados na variável plotada no eixo y (como já vimos em um gráfico de densidade em seção anterior).
Para avaliarmos se esse é mesmo o caso, acrescentamos linhas de tendência nos dados por grupo, usamos a camada geom_smooth(), que plota a linha de regressão de y em x (linhas 107 a 110).
Além disso, modificamos manualmente as cores dos pontos do nosso gráfico (linhas 111 a 113), os títulos dos eixos (linhas 114 a 116) e a posição da legenda no gráfico (linha 117). A Figura 14 apresenta o gráfico resultante do código a seguir.
# gráfico 12
ggplot(dados1, aes(x = x,
y = y)) +
geom_point(size = 1.5,
aes(color = grupo)) +
geom_smooth(method = "lm",
se = FALSE,
aes(group = grupo),
color = "gray10") +
scale_color_manual(
values = c("A" = "slateblue", s
"B" = "violet")) +
labs(color = "grupo",
x = "Preditora",
y = "Resultado") +
theme(legend.position = "bottom")

Notamos agora que o relacionamento entre as variáveis (denominadas de Preditora e Resultado no último gráfico) é similar para os dois grupos, isto é, as duas linhas de tendência têm inclinações paralelas. Contudo, o fato de os interceptos serem diferentes denota que os escores médios do grupo B na variável Resultado é maior que os escores médios do grupo A.
Criando dados sintéticos no R (Parte 2)
O segundo conjunto de dados (dados2) contém quatro colunas, sendo uma longitudinal (tempo), em três níveis (pré-teste, pós-teste e follow-up); uma grupal (grupo), em dois níveis (experimental e controle); e uma variável dependente (depressao). A quarta coluna representa a margem de erro (MOE), que pode ser usada para criar barras de erro representando intervalos de confiança.
# cria novos dados simulando uma variável de grupo (grupo)
# e uma variável longitudinal (tempo)
dados2 <- data.frame(
tempo = rep(c("Pré-Teste",
"Pós-Teste",
"Follow-Up"),
2),
grupo = rep(c("Experimental",
"Controle"),
each = 3),
depressao = c(45, 30, 35, 46, 48, 47),
MOE = c(3, 2, 2, 3, 3, 2)) confiança)
dados2$tempo <- factor(dados2$tempo,
levels = c("Pré-Teste",
"Pós-Teste",
"Follow-Up"))
A Figura 15 apresenta as 6 linhas dos dados2. Entretanto, é importante notar que, nesses dados, cada linha representa as médias de uma condição, e não os escores de participantes individuais.

dados2. Como construir gráficos de barras no R com o ggplot2?
Em delineamentos experimentais, dois tipos de gráficos comumente usados são os gráficos de barras e de linhas, pois eles permitem apresentar as médias para cada condição experimental. Primeiramente, abordaremos os gráficos de barras. Em seguida, falaremos sobre os gráficos de linhas.
Criando um gráfico de barras básico no R
A partir do próximo código, passamos a usar os dados2. Aqui especificamos os novos nomes das variáveis de dados2 para o mapeamento estético, aes(). Indicamos quais variáveis serão plotadas em cada eixo (linhas 139 e 140), e a camada geom_bar() nos permite plotar, para cada valor de tempo, o escore médio contido em depressao (linha 141). A Figura 16 apresenta o gráfico resultante do código a seguir.
# gráfico 13
ggplot(dados2, aes(x = tempo, # variável tempo no eixo x
y = depressao)) + # variável depressao no eixo y
geom_bar(stat = "identity")

Criando gráficos de barras personalizados no R
Embora as barras dos diferentes grupos tenham cores distintas na Figura 16, a escolha por tons de cinza dificulta bastante diferenciar as fronteiras entre as categorias. Por isso, visando melhorar a discriminação visual dos diferentes grupos, acrescentamos, no próximo código, que o preenchimento deverá ser distinto para cada grupo (linha 146). A Figura 17 apresenta o gráfico resultante do código a seguir.
# gráfico 14
ggplot(dados2, aes(x = tempo,
y = depressao,
fill = grupo)) +
geom_bar(stat = "identity")

Embora a visualização tenha melhorado, o empilhamento das barras dificulta comparar os grupos nos diferentes tempos. Isso ocorre porque, por padrão, geom_bar() recebe o argumento “stack” em position. Felizmente, podemos modificar esse comportamento (linha 154).
Para melhorar ainda mais a visualização, podemos, por exemplo, acrescentar intervalos de confiança às barras. Isso é feito por meio da camada geom_errorbar(), modificamos as espessuras das barras (linhas 158 a 161) e acrescentamos títulos dos eixos (linhas 162 e 163). A Figura 18 apresenta o gráfico resultante do código a seguir.
# gráfico 15
ggplot(dados2, aes(x = tempo,
y = depressao,
fill = grupo)) +
geom_bar(stat = "identity",
position = position_dodge(),
width = 0.7,
color = "black",
size = 1) +
geom_errorbar(aes(ymin = depressao - MOE,
ymax = depressao + MOE),
width = 0.2,
position = position_dodge(0.7)) +
labs(x = "Tempo",
y = "Escore de Depressão")

A Figura 18 deixa as tendências dos dados mais claras: para o grupo experimental, por exemplo, os níveis de depressão parecem ter diminuído do pré- para o pós-teste, e se mantido razoavelmente no follow-up. Por outro lado, no grupo controle, os níveis de depressão parecem não terem mudado substancialmente ao longo do tempo. Todavia, tais efeitos precisariam ser avaliados adicionalmente por meio de estatística inferencial, o que vai além do escopo deste tutorial.
Como construir gráficos de linhas no R com o ggplot2?
Criando um gráfico de linhas básico no R
Alguns pesquisadores preferem plotar variáveis que denotam o tempo como pontos ligados por linhas, pois isso facilita visualizar a tendência dos dados em delineamentos longitudinais. Os mesmos dados anteriores serão usados a seguir para representar gráficos de linhas.
Para isso, vamos inserir uma camada com a geometria geom_line(), com cores (linha 170) e tipos (linha 169) de linhas distintas por grupo. A Figura 19 apresenta o gráfico resultante do código a seguir.
# gráfico 16
ggplot(dados2, aes(x = tempo,
y = depressao,
group = grupo)) +
geom_line(aes(linetype = grupo,
color = grupo),
size = 1)

Em seguida, vamos melhorar a estética do gráfico. Nesse exemplo, iremos acrescentar uma camada com pontos indicando as médias por grupo e tempo. Isso será feito combinando geom_line() com geom_point(), que já vimos em seção anterior. A Figura 20 apresenta o gráfico resultante do código a seguir.
# gráfico 17
ggplot(dados2, aes(x = tempo,
y = depressao,
group = grupo)) +
geom_point(aes(shape = grupo,
color = grupo),
size = 3) +
geom_line(aes(linetype = grupo,
color = grupo),
size = 1)

Agora o grupo experimental é representado por triângulos e linhas tracejadas azuis, enquanto o grupo controle é representado por círculos e linhas contínuas rosas.
Por fim, melhoraremos a apresentação do gráfico acrescentando barras de erro, representando intervalos de confiança. Isso será feito, mais uma vez, por meio da geometria geom_errorbar(). Além disso, também faremos várias modificações estéticas, para personalizar nosso último gráfico. A Figura 21 apresenta o gráfico resultante do código a seguir.
# gráfico 18
ggplot(dados2, aes(x = tempo,
y = depressao,
group = grupo)) +
geom_point(aes(shape = grupo,
color = grupo),
size = 3) +
geom_line(aes(linetype = grupo,
color = grupo),
size = 1) +
geom_errorbar(aes(ymin = depressao - MOE,
ymax = depressao + MOE),
width = 0.2,
color = "gray20") +
scale_shape_manual(values = c(16, 21)) +
scale_size_manual(values = c(8, 8)) +
labs(x = "Tempo",
y = "Escore de Depressão") +
scale_y_continuous(limits = c(25, 55)) +
theme_minimal() +
theme(
# Formatação do título do eixo x
axis.title.x = element_text(size = 12,
face = "bold"),
# Formatação do título do eixo y
axis.title.y = element_text(size = 12,
face = "bold"),
legend.position = "bottom",
legend.title = element_blank())

Conclusão
Neste post, apresentamos uma introdução de como criar gráficos no R. Se você ficou interessado em criar gráficos elegantes, personalizados e de alta qualidade, mas ainda não é um usuário do R, então veja a novidade que preparamos a seguir!
É com grande satisfação que a Psicometria Online anuncia o curso R para Iniciantes. O curso tem como objetivo abordar todos os tópicos essenciais do R, permitindo assim que você explore assuntos específicos sem ser prejudicado por dúvidas básicas. Se você trabalha com pesquisa científica e deseja aprender a utilizar o R, então o curso R para Iniciantes é para você.

Além disso, se você quer saber mais sobre a Psicometria Online Academy, acesse nosso site. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Wilkinson, L. (2005). The grammar of graphics (2nd ed.). Springer.
Como citar este post
Lima, M. (2024, 8 de julho). Como criar gráficos no R com o ggplot2? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-criar-graficos-no-r-com-o-ggplot2/













