Neste post, exploraremos o conceito de covariância. O post se dividirá em quatro seções principais. Inicialmente, definiremos o que é covariância. A seguir, apresentaremos sua fórmula, relacionando-a à fórmula da variância. Depois, apresentaremos uma intuição do significado geométrico dessa medida. Por fim, nós compararemos os conceitos de covariância e de correlação.

Qual é a definição de covariância?
A covariância é uma medida que expressa o grau de interdependência linear entre duas variáveis. Desse modo, podemos pensar nessa medida como um índice de variabilidade conjunta, que indica se a variabilidade das duas variáveis possui alguma tendência. Em outras palavras, a covariância quantifica o quanto uma variável se altera em resposta às mudanças em outra variável.
No caso da covariância positiva, quando os valores de uma variável aumentam, os valores da outra também tendem a aumentar. A Figura 1 ilustra essa situação. Por exemplo, considere as variáveis idade e salário. Nesse caso, é provável que, conforme a idade aumenta, o salário também aumente.

Por outro lado, na covariância negativa, o aumento nos valores de uma variável implica o decréscimo nos valores da outra variável. A Figura 2 ilustra esse cenário. Por exemplo, considere as variáveis temperatura e venda de roupas de frio. Nesse caso, é provável que, conforme a temperatura aumenta, a venda de roupas de frio tenda a cair.

Por fim, existem situações em que duas variáveis têm covariância nula, isto é, elas não estão relacionadas entre si. A Figura 3 ilustra essa possibilidade. Por exemplo, considere as variáveis cotação do dólar e número de passos que você dá ao longo do dia. Nesse caso, a menos que você trabalhe na Bolsa de Valores e seja diretamente afetado pela cotação do dólar, é extremamente improvável que essas duas variáveis covariem.

Como é calculada a covariância?
Para entendermos a fórmula da covariância, é útil fazermos uma analogia com a fórmula da variância. A fórmula da variância (s2) é dada por:

onde x representa o escore da observação i em uma amostra, X-barra representa a média amostral, e N representa o tamanho amostral.
Tenha em mente que a diferença entre um escore e a média (o termo entre parênteses) é um desvio, e que esse valor ao quadrado é denominado desvio quadrático. Sendo assim, variância fornece um índice de variabilidade dos dados, em unidades quadráticas.
Uma maneira alternativa de expressar a fórmula da variância é expandindo o quadrado do numerador:

As duas fórmulas são conceitualmente idênticas, mas, nesta última, o expoente foi substituído pela repetição do fator que está sendo elevado ao quadrado. Embora essa apresentação seja pouco convencional em livros-textos, ela é útil para os objetivos deste post. Especificamente, ela guarda similaridade com a fórmula da covariância:

onde x e y representam os escores de cada observação i em uma amostra nas variáveis X e Y, e X-barra e Y-barra representam as médias amostrais nas duas variáveis; N representa, mais uma vez, o tamanho amostral.
Você deve ter notado que as fórmulas são quase idênticas. No entanto, ao invés de elevarmos os desvios ao quadrado (como na fórmula da variância), o que fazemos na fórmula da covariância é multiplicar os desvios de cada participante em duas variáveis distintas (i.e., produtos dos desvios ou desvios cruzados). É por considerar duas variáveis distintas simultaneamente, portanto, que essa medida expressa a variabilidade conjunta de duas variáveis.
Como interpretar a covariância?
Destrinchando um diagrama de dispersão
A seguir, nosso objetivo é fornecer uma intuição geométrica do que a covariância nos informa. A Figura 4 representa um diagrama de dispersão, mas temporariamente sem dados plotados. Esse diagrama contém duas linhas pontilhadas vermelhas, que serão úteis para nosso entendimento da covariância.

A linha vertical vermelha representa a média amostral da variável X. Isso significa que pontos plotados à esquerda da linha vertical representam participantes que estão abaixo da média em X, enquanto pontos à sua direita representam participantes acima da média em X.
Por outro lado, a linha horizontal representa a média de uma amostra na variável plotada no eixo Y. De maneira similar, isso significa que pontos acima da linha horizontal representam participantes acima da média em Y, enquanto pontos abaixo dela representam participantes abaixo da média em Y.
Como já visto, a fórmula da covariância calcula, em seu numerador, os desvios de duas variáveis em relação às médias e depois multiplica esses desvios. Pelas regras da multiplicação, sabemos que desvios com sinais iguais resultarão em um valor positivo, enquanto que desvios com sinais diferentes resultarão em um valor negativo.
Desvios com sinais iguais são observações que estão acima da média nas duas variáveis (quadrante B) ou abaixo da média nas duas variáveis (quadrante C). Por outro lado, desvios com sinais diferentes são observações que estão acima da média em uma variável, mas não na outra (quadrantes A e D).
Significado geométrico da covariância
O segredo para entender a fórmula da covariância é pensar que ela reflete como os quadrantes da Figura 4 são preenchidos pelas observações da amostra. A seguir, reapresentamos os diagramas de dispersão das Figuras 1, 2 e 3 na Figura 5, mas agora contendo as linhas pontilhadas representando as médias das variáveis em cada eixo.
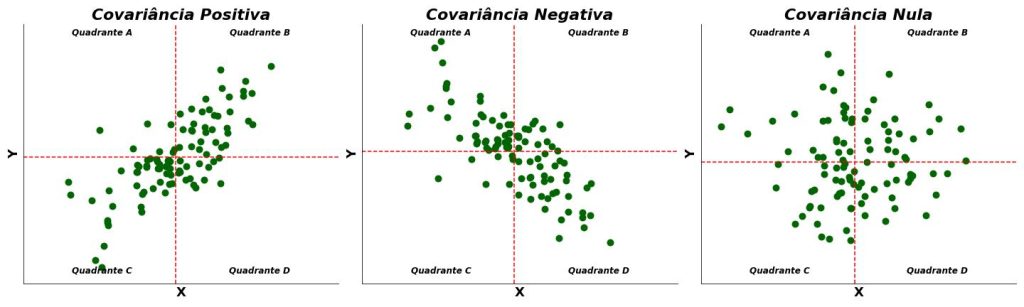
Observe que no caso da covariância positiva, os quadrantes B e C possuem a maior densidade de pontos (Figura 5, painel esquerdo). Lembrando, esses são os quadrantes cujos desvios terão sinais iguais, resultando em desvios cruzados positivos. Quanto mais desvios cruzados positivos tivermos, maior será o valor da covariância.
Por outro lado, no caso da covariância negativa, os quadrantes A e D têm a maior densidade de pontos (Figura 5, painel central). As observações nesses quadrantes têm desvios com sinais diferentes, resultando em desvios cruzados negativos. Quanto mais desvios cruzados negativos tivermos, menor (i.e., mais negativo) será o valor da covariância.
Por fim, no caso da covariância nula (Figura 5, painel direito), os pontos parecem se distribuir de maneira igualmente frequente nos quatro quadrantes, formando um padrão aproximadamente circular. Consequentemente, os desvios cruzados positivos (quadrantes B e C) e os negativos (quadrantes A e D) se anulam, quando somados. É por isso que a fórmula da covariância resulta em um valor próximo a zero quando os dados apresentam esse padrão geométrico.
Em síntese, a covariância representa a variabilidade conjunta de duas variáveis, indicando se elas possuem alguma tendência linear. Essa tendência pode ser representada geometricamente pelas distintas densidades de pontos em diferentes quadrantes de um diagrama de dispersão e, numericamente, por meio de valores positivos, negativos ou nulos de covariância.
Covariância é a mesma coisa que correlação?
Neste momento, você pode estar se perguntando se covariância é a mesma coisa que correlação. De fato, os dois conceitos estão intimamente ligados, mas eles não são sinônimos.
A covariância é uma medida não padronizada da variabilidade conjunta das variáveis. Sendo assim, ela gera resultados que dependem dos valores das variáveis na escala original, o que torna sua interpretação mais difícil. Por exemplo, se uma das variáveis de interesse for expressa em centímetros, metros ou quilômetros, os valores de covariância mudarão.
Por outro lado, a correlação de Pearson – a medida de correlação mais conhecida por pesquisadores – consiste em uma medida padronizada de variabilidade conjunta. Em outras palavras, ela é calculada como a covariância dividida pelos desvios padrões das duas variáveis de interesse. Isso faz com que seus valores sempre estejam entre –1 e +1, independentemente da escala original das variáveis de interesse.
Para concluir, dada a íntima relação entre essas duas medidas, a intuição geométrica da covariância que apresentamos nesse post também se aplica ao conceito de correlação.
Conclusão
Neste post, você aprendeu o que é covariância e que ela é importante por ser a base da correlação, além de se fazer presente em outras análises quantitativas, como na modelagem por equações estruturais.
Esperamos que este post tenha ajudado você a entender melhor o conceito de covariância. Aproveite e se inscreva em nosso canal do YouTube para aprimorar suas habilidades em análise de dados!
Gostou desse conteúdo? Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Cumming, G. (2012). Correlations, proportions, and further effect size measures. In G. Cumming, Understanding the new statistics: Effect size, confidence intervals, and meta-analysis (pp. 381–410). Routledge.
Como citar este post
Lima, M. (2021, 14 de março). O que é covariância? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-covariancia/














