Curva característica do item, curva de informação do item e curva de informação do teste
Se você já ouviu falar em teoria de resposta ao item, então provavelmente encontrou os termos curva característica do item, curva de informação do item e curva de informação do teste. Neste post, vamos explicar de forma acessível o que significam essas três curvas.
Primeiramente, apresentamos uma visão geral da teoria de resposta ao item e da curva característica do item. Em seguida, mostramos como interpretar a curva de informação do item. Depois, discutimos a curva de informação do teste e suas aplicações. Por fim, trazemos dois exemplos práticos de como utilizar essas curvas em contextos reais.

Curva característica do item: fundamentos da teoria de resposta ao item
A curva característica do item é uma representação gráfica que mostra a probabilidade de um respondente acertar ou endossar um item em função de sua habilidade — representada pela letra grega theta, θ. Essa curva é uma das bases da teoria de resposta ao item (TRI), um modelo amplamente usado na psicometria.
Ao analisar uma curva característica do item, você obtém informações sobre:
- A dificuldade do item, isto é, a posição da curva no eixo da habilidade.
- A discriminação do item, ou seja, o quanto o item diferencia pessoas com níveis de habilidade próximos (representada pela inclinação da curva).
- O acerto ao acaso, útil em itens de múltipla escolha (assíntota inferior da curva).
- E, em modelos mais avançados, o erro por distração (assíntota superior da curva).
Esses parâmetros ajudam a entender como cada item se comporta dentro de um teste. Como resultado, você pode selecionar ou revisar itens com mais embasamento técnico.
A Figura 1 apresenta cinco curvas características dos itens. A fim de simplificar nossa discussão, o único parâmetro que difere entre as curvas é o parâmetro de dificuldade (representado pela letra grega delta, δ). Itens mais à esquerda (δs menores) são mais fáceis, enquanto itens mais à direita (δs maiores) são mais difíceis de serem acertados ou endossados.
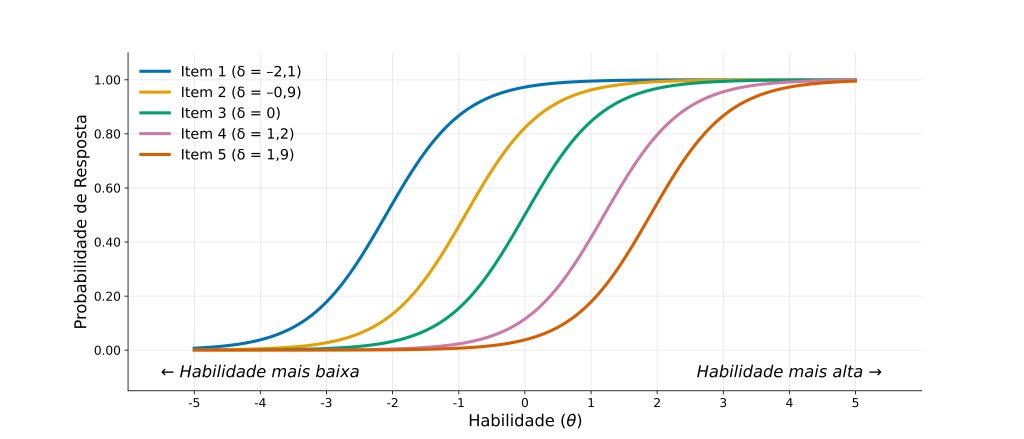
Portanto, conhecer e saber interpretar a curva característica do item é um passo essencial para construir instrumentos válidos, fidedignos e justos.
Curva de informação do item: complementando a curva característica do item
A curva de informação do item mostra quanto um item contribui para medir as habilidades de respondentes localizados em diferentes pontos do continuum de habilidade.
Em outras palavras, enquanto a curva característica do item mostra a probabilidade de acerto, a curva de informação do item mostra o quanto aprendemos sobre diferentes respondentes com a resposta a esse item.
Itens diferentes têm diferentes “zonas” de maior informação. Por exemplo:
- Um item muito fácil (δ menor) fornece mais informação para respondentes com baixa habilidade (θs menores).
- Um item mais difícil (δ maior), por outro lado, será mais informativo para respondentes com alta habilidade (θs maiores).
A Figura 2 apresenta curvas de informação dos cinco itens já mencionados na seção anterior. As formas das curvas geralmente se parecem com uma distribuição normal. Note que o pico de cada uma delas indica onde cada item é mais preciso — ou seja, onde ele mais “informa” sobre a habilidade do respondente.
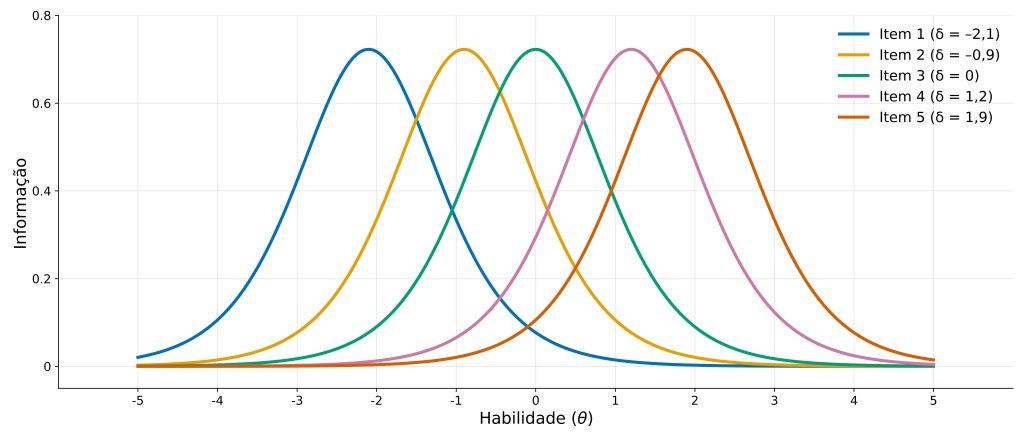
Desse modo, na Figura 2, o local onde cada item é mais informativo coincide com o valor de dificuldade (δ) do item. Isso acontece porque modelamos apenas esse parâmetro em nosso exemplo.
Por fim, é importante ressaltar que as curvas de informação do itens nos ajudam a decidir quais itens devem compor um teste, dependendo da população-alvo.
Por exemplo, se estamos amostrando uma população clínica, com escores mais elevados, devemos incluir itens mais “fortes”, cujas curvas de informação dos itens indiquem que eles são mais informativos para respondentes com maior traço latente.
Dessa forma, analisar a curva de informação do item é uma etapa estratégica na construção de qualquer avaliação baseada em TRI.
Curva de informação do teste: a visão global das curvas características dos itens
A curva de informação do teste é o somatório das curvas de informação dos itens de todos os itens de um teste. Com ela, visualizamos a fidedignidade do teste como um todo ao longo dos diferentes níveis de habilidade.
Quanto maior a curva de informação do teste em um ponto da escala, maior a fidedignidade da medida naquele nível. Isso é crucial para garantir que o teste seja adequado ao público-alvo. Por exemplo:
- Um teste com curva de informação do teste concentrada entre θ = –1 e θ = 1 será muito precisa para respondentes de habilidade média, mas impreciso para os extremos.
- Já um teste com curva de informação do teste ampla cobre bem todas as faixas de habilidade, sendo ideal para populações heterogêneas.
A Figura 3 apresenta a curva de informação do teste, considerando os cinco itens mostrados nas seções anteriores. Como os itens individualmente eram informativos em diferentes regiões entre δ = –2,1 e δ = 1,9, o teste parece ser altamente informativo nessa faixa de θs.
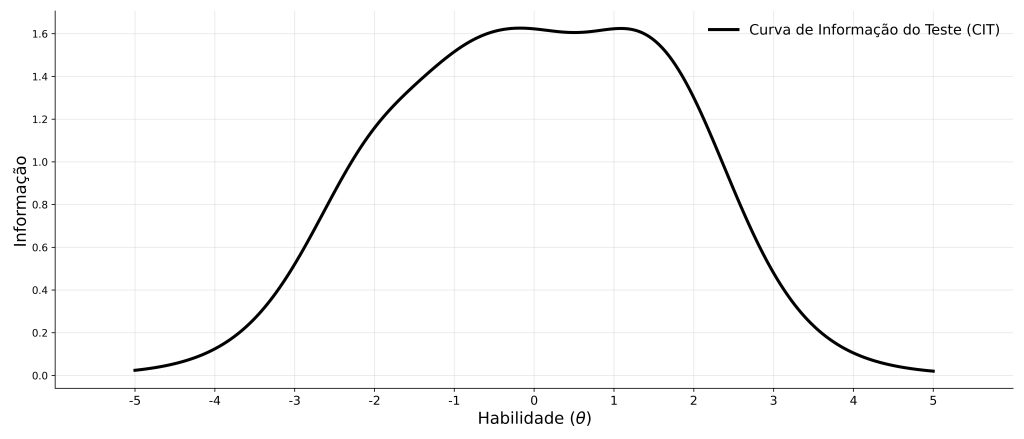
Assim como as curvas de informação dos itens ajudam a selecionar itens individualmente, a curva de informação do teste permite avaliar a qualidade do conjunto. Com base nisso, você pode comparar diferentes versões de um teste, ajustar itens ou verificar lacunas de informação.
Portanto, usar a curva de informação do teste torna sua construção de testes muito mais estratégica e baseada em evidências.
Saiba mais: Vantagens da TRI sobre a teoria clássica dos testes

Exemplos práticos: usando as curvas na avaliação
Exemplo 1: selecionando itens para um teste educacional
Imagine que você é um professor de matemática. Ao criar uma avaliação, você pode usar as curvas características dos itens para identificar quais questões discriminam melhor os alunos. Em seguida, ao observar as curvas de informação dos itens, você escolhe perguntas que oferecem mais informação no intervalo de habilidades da sua turma.
Com isso, o teste final, analisado pela curva de informação do teste, será fidedigno onde mais importa — garantindo uma avaliação justa e eficaz.
Exemplo 2: avaliação psicológica ou organizacional
Agora, imagine que você trabalha com seleção de pessoal. Você aplica um teste de comunicação oral e gera as curvas características dos itens, as curvas de informação dos itens e a curva de informação do teste. As curvas mostram em que faixa de habilidade o teste é mais preciso e quais itens contribuem de fato para esse fim.
A partir dessas análises, você pode ajustar o teste e obter uma medida muito mais fidedigna das competências dos candidatos. Isso impacta diretamente na qualidade da decisão final.
Conclusão
Gostou deste conteúdo? Então aproveite e também se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Como citar este post
Lima, M. (2025, 6 de junho). Curva característica do item, curva de informação do item e curva de informação do teste: como interpretar as três curvas da TRI? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/curva-caracteristica-do-item-curva-de-informacao-do-item-e-curva-de-informacao-do-teste/














