O que é eta ao quadrado?

Neste post, explicaremos o que é o eta ao quadrado (η²). Primeiramente, definiremos e mostraremos como calcular o eta ao quadrado. Em seguida, falaremos sobre o eta parcial ao quadrado (η²_p), seu cálculo e suas limitações. Por fim, nós apresentaremos diretrizes de como interpretar os valores do η².

O que é o eta ao quadrado?

O eta ao quadrado (η²) é uma medida de tamanho do efeito utilizada nas análises de variância (ANOVAs). Em síntese, essa métrica indica a proporção da variância total da variável dependente que pode ser atribuída à variável de grupo (isto é, à variável independente). De modo geral, o η² integra a família de medidas r de efeito e funciona como uma extensão do r².

Como calcular o eta ao quadrado?

A fórmula do eta ao quadrado é de simples compreensão:

Nessa equação, SQ_efeito​ representa a soma dos quadrados do efeito de interesse, enquanto SQ_total​ corresponde à soma total dos quadrados, incluindo efeitos, erros e interações.

Enquanto o SQ_total expressa a variabilidade total dos escores em torno da média geral da amostra (ignorando os grupos), o SQ_efeito corresponde à parte dessa variabilidade que as diferentes médias grupais conseguem explicar.

O que é o eta parcial ao quadrado?

Embora semelhantes, eta ao quadrado e eta parcial ao quadrado (η²_p) não são a mesma coisa. O η² é útil para comparar tamanhos de efeito dentro de um mesmo estudo, já que todos os valores somam 1. Contudo, ele não é ideal para comparações entre estudos, pois sua métrica depende do número e da natureza das variáveis do modelo.

A fim de contornar essa limitação, Keppel (1991) recomendou o uso do η²_p. Nessa medida, os efeitos de outras variáveis independentes e suas interações são parcialmente eliminados, tornando os resultados mais comparáveis entre estudos diferentes.

A fórmula do η²_p é:

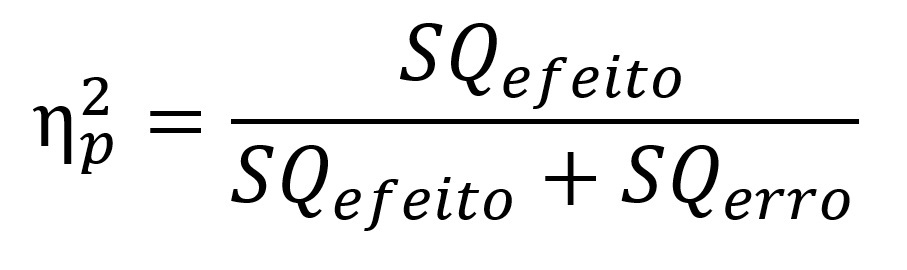
Assim, o η²_p expressa a proporção de variância explicada pelo efeito de interesse em relação à soma entre ele e o erro associado. Em outras palavras, ele representa a proporção de variância explicada por um fator específico, considerando apenas o erro associado a ele e ignorando parcialmente a contribuição dos demais fatores no modelo.

Limitações do eta parcial ao quadrado

Apesar de vantajoso, o eta parcial ao quadrado tem limitações importantes. Por exemplo, ele pode variar conforme o delineamento do estudo. Quando comparamos as mesmas duas médias em ANOVA de medidas repetidas e em ANOVA de medidas independentes, o η²_p tende a ser maior no primeiro caso — especialmente se houver correlação positiva entre os grupos.

Além disso, diferenças na inclusão de covariáveis podem afetar o η²_p (Olejnik & Algina, 2003). Assim, seu uso deve ser feito apenas em estudos com planejamentos experimentais semelhantes.

Para lidar com essa limitação, Olejnik e Algina (2003) propuseram o uso do eta generalizado ao quadrado (η²_G). Essa alternativa exclui a variação causada por outros fatores e inclui a variação individual — tornando-a, portanto, mais comparável entre delineamentos diferentes, como estudos entressujeitos e intrassujeitos.

Como interpretar o eta ao quadrado?

Cohen (1988) propôs valores de referência para a interpretação do eta ao quadrado:

• Pequeno: η² < 0,01.
• Médio: η² entre 0,02 e 0,06.
• Grande: η² > 0,14.

O η² varia entre 0 e 1 e, se multiplicado por 100, pode ser interpretado como porcentagem de variância explicada. Por exemplo, um η² de 0,13 indica que 13% da variância total pode ser atribuída à variável de grupo.

Já o η²_p também varia entre 0 e 1, mas não deve ser interpretado como porcentagem da variância total, pois considera apenas a variância explicada em relação ao erro do efeito específico. De fato, a soma dos η²_p de diferentes efeitos pode ultrapassar 1, o que compromete que ele seja interpretado de maneira similar ao η² (Richardson, 2011).

Ainda assim, é importante destacar que você deve usar os pontos de corte apenas como último recurso. Sempre que possível, relacione o tamanho do efeito com resultados semelhantes da literatura de sua área de pesquisa.

Conclusão

Muitos artigos relatam ter utilizado o η², quando, na realidade, calcularam o η²_p. Um indício comum desse erro é quando a soma dos η²_p de diferentes efeitos ultrapassa 1 — algo possível apenas no η²_p (Pierce et al., 2004).

Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).

Referências

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2^nd ed.). Erlbaum.

Keppel, G. (1991). Design and analysis: A researcher’s handbook (3^rd ed.). Prentice-Hall.

Olejnik, S., & Algina, J. (2003). Generalized eta and omega squared statistics: Measures of effect size for some common research designs. Psychological Methods, 8, 434–447. https://doi.org/10.1037/1082-989X.8.4.434

Pierce, C. A., Block, R. A., & Aguinis, H. (2004). Cautionary note on reporting eta-squared values from multifactor ANOVA designs. Educational and Psychological Measurement, 64(6), 916–924. https://doi.org/10.1177/0013164404264848

Richardson, J. T. E. (2011). Eta squared and partial eta squared as measures of effect size in educational research. Educational Research Review, 6(2), 135-147. https://doi.org/10.1016/j.edurev.2010.12.001

Como citar este post

Damásio, B. (2021, 31 de maio). O que é eta ao quadrado? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/eta-ao-quadrado/